Problems of Monomorphism and Epimorphism in Discrete mathematics

Monomorphism

A monomorphism can be described as an injective homomorphism in the context of universal algebra or abstract algebra. Monomorphism is also known as mono or monic morphism. The following notation is used to show the monomorphism from X to Y:

Suppose there are two objects, X and Y, and another object Z. A morphism f from X to Y will be known as monomorphism if for Z and for any pair of morphism g1 and g2 from object Z to an object X, it satisfies the condition, i.e., "if fg1 = fg2, then g1 = g2". In place of called f as monomorphism, some people say 'f is monic' or 'f is mono'.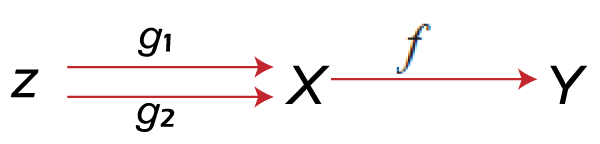

If there is a case where a morphism f is monic, we have the ability to cancel it out on the left. To do this, we can follow the sense of fg as described above.

The monomorphism is a type of dual concept to epimorphism, which means that in category C, a monomorphism is an epimorphism in the dual category Cop. So mono is every section, and epimorphism is every retraction.

Monomorphism can also describe as a categorical generalization of injective functions. This injective function is also known as the one-to-one function. So the injective and one-to-one both are the same, but injective is a French name, and one-to-one is a German name. This injective term replaced this one-to-one in a large amount. In some categories, the term injective does not correspond to their traditional counterparts, but in the remaining categories, they do. The term monomorphism is more general.

Relation to invertibility

The left invertible morphisms will be known as necessarily monic: if l is the left inverse for f, in this case, f is monic as

A left invertible morphism is also known as the split mono.

However, there is no requirement of monomorphism to be left invertible. For example: Suppose there is a category Group of all group, and there is also group morphisms among them. If there is a case where H is a subgroup of G, then the inclusion f : H → G is always a monomorphism. But if H contains a normal complement in G, in this case, f will contain a left inverse in the category.

Example:

Every morphism will be a monomorphism if it is in a concrete category in, which the underlying function is injective. We can also describe this concept with the help of some other words. According to this, if morphisms are is used to describe the functions between the sets, then in a categorical sense, any morphism which is an injective function will surely be a monomorphism. The converse will also hold in the category of sets, so we can say that monomorphisms are exactly the injective morphisms. The categories of algebras also contain the converse. This is because we have a free object on one generator. In other types of categories, such as any abelian category, all rings, and all groups, this statement will also be true.

Properties:

• In a topos, every monic will be an equalizer, and if there is any map that contains both epic and monic, then it will be an isomorphism.
• Every isomorphism will be monic.

Epimorphism

An epimorphism can be described as a surjective homomorphism or onto in the context of universal algebra or abstract algebra. The monomorphism is also known as epic morphism or epi. The following notation is used to show the epimorphism:

Suppose there are two objects, X and Y, and another object Z. So a morphism f from X to Y will be known as epimorphism if for Z and for any pair of morphism g1 and g2 from object Y to an object Z, it satisfies the condition, i.e., "if g1f = g2f, then g1 = g2". In place of called f as epimorphism, some people say 'f is epic' or 'f is epi'.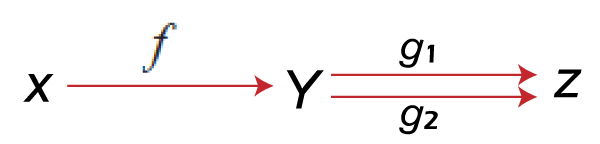

If there is a case where a morphism f is epic, we have the ability to cancel it out on the right. To do this, we can follow the sense of fg as described above.

Unfortunately, we are able to conventionally write the composition of a function from right side to left side. In the above image, we can see that f exits on the left side, and composition proceeds from left to right. But if we try to write the composition of functions, we always choose to write it from right to left, i.e., gf. When we talk about cancel out f from right, we are not talking about the right of a commutative diagram. We actually mean about the right of expression gf.

Epimorphisms can also be described as analogues of injective functions, but both concepts are not exactly the same. There are some differences between them. The monomorphism is a type of dual concept of epimorphism, which means that in category C, an epimorphism is a monomorphism in the dual category Cop.

In the algebraic sense, every epimorphism will be an epimorphism in the sense of category theory, but in all the other categories, the converse of this statement will not be true. So, in conclusion, we can say that in this section, we are using the term epimorphism in the sense of category theory.

Examples

In a concrete category, every morphism will be an epimorphism if there is an underlying function of morphism which is surjective. The converse of this is also true in various types of concrete categories of interest. For example: Here, we will have the various categories in which epimorphisms will be exactly those types of morphisms that are surjective or onto on the underlying sets, which is described as follows:

Sets:

It can be described as sets and functions. If we want to prove that every epimorphism f: X → Y is surjective in a set, we can do this by composing it with both categories. In first one, the function g1: Y → {0, 1} of the image f(x), and in the second one, map g2: Y → {0, 1} that is constant 1.

Rel:

It can be described as sets with binary relations and relations preserving functions. Here the same proof that we have used in the Set can be used. The above proof will provide {0, 1} with the full relation {0, 1} * {0, 1}.

Pos:

It can be described as partially ordered sets and also monotone functions. If there is a case where f: (X, ?) → (Y, ?) is not surjective, then we will pick yo in Y/f(X) and assume the two things. The first one is that g1: Y → {0, 1} be the characteristics function of {y | y0 ? y}, and the second one is that g2: Y → {0, 1} be the characteristics function of {y | y0 < y}. If {0, 1} provides us a standard ordering 0 < 1, then these two maps will be monotone.

Grp:

It can be described as group and group homomorphism. With the help of Otto Schreier, the successful result related to every epimorphism is surjective in Group is occurred. In Linderholm 1970, we can find elementary proof about this.

FinGrp:

It can be described as finite group and group homomorphism. With the help of Schreier, we can also establish the proof in this case also, which is given in Linderholm 1970.

Ab:

It can be described as an abelian group and group homomorphism.

K-Vect:

It can be described as vector spaces over a field and also a K linear transformation.

Mod- R:

It can be described as the right modules over a ring R and also a module homomorphism. Here we will prove that in a Mod-R, every epimorphism f: X → Y is surjective with the help of generalizing the above two examples. To do this, we will compose this epi with both the canonical quotient map g1: Y → Y / f(X) and the zero maps g2: Y → Y/f(X).

Top:

It can be described as topological spaces and continuous functions. We will use the same process as we have used in the Set to prove that every epimorphism is surjective in Top. The set will provide us {0, 1}. Here we will use the indiscrete topology, which is used to make sure that all the considered maps are continuous.

HComp:

It can be described as a compact Hausdorff space and also continuous functions. If there is a case where f: X → y is not surjective, then we will assume y in Y-fX. Since we know that Fx is closed. With the help of Urysohn's Lemma, it contains a continuous function g1: Y → {0, 1} in such a way that g1 is 0 and fX and 1 on y. Lastly, we will compose f with both zero function g2: Y → {0, 1}, and with g1.

Epimorphism also contains a lot of concrete categories in which they fail to be surjective. Some of these categories are described as follows:

Mon:

It can be described as Monoid. A non-surjective epimorphism is shown by the inclusion map N → Z in the category of monoids. We can prove this by assuming the two distinct maps g1 and g2 from Z to some monoid M. Suppose there is some n in Z. In this case, g1(n) ? g2(n), so g1(-n) ? g2(-n). So we have seen that either n or -n is in N. So, there is an unequal amount of restriction of g1 and g2 to N.

Ring:

A non-surjective epimorphism can be shown by the inclusion map Z → Q in the category of rings. We are able to determine any ring homomorphism on Q with the help of determining its action on Z.

Haus:

It can be described as Hausdorff spaces. The epimorphism can be described as the continuous functions, which contains the dense images in the category of Hausdorff spaces. For example: A non-surjective epimorphism can be shown by the inclusion map Q → R

Similarities and differences between monomorphism and epimorphism

In any category, an isomorphism is monomorphism and also epimorphism. In other words, we can say that an iso is monic and also epic. In some categories, the converse of this will hold, but in other categories, it will not hold.

Sets and Groups

A function f from object X to an object Y will be known as epimorphism in the category of sets if it is surjective. Same as a function will be monomorphism in the category of sets iff it is injective.

The categories of groups are also similar, which means a group homomorphism will be a monomorphism if it is injective, and it will also epimorphism if it is surjective.

Monoids

Recall that a monoid is the same as a group, but it is not necessary that we have an inverse. That means here, we will have an associative operation and an identity element.

For this, we will assume a non-negative integer N containing addition, and also assume the integers Z. After that, we will assume an inclusion map f which takes N into Z. In this case, f will be monomorphism and injective. This map is homomorphism but not surjective. This is because we can determine the homomorphism from integers to another monoid with the help of finding out its values on the positive integers. Half of the codomain can still contain in its range, but we have the ability to cancel it out on the right.

So lastly, there is a function which is monomorphism and epimorphism, but it will not be an isomorphism.

Ring

A ring homomorphism will be known as mono if it is injective. But in the case of monoids, the ring homomorphism does not need to be surjective to be epimorphism.

For example: Here, we can find out the ring homomorphism with the help of determining its values on integers. We will take the inclusion map from integers to rationals. So we can say that the inclusion map is an epimorphism without caring that it is surjective or not.

Incidentally, homomorphism between the fields is monic.