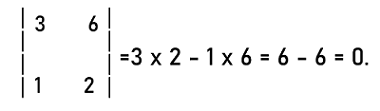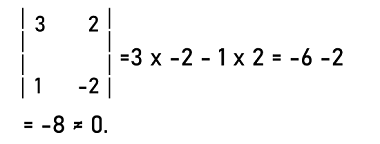Singular matrix in Discrete mathematicsWe can find that the given matrix is singular or non-singular with the help of finding the determinant of the matrix. With the help of symbol |A| or det A, we can indicate the determinant of matrix A. The matrix will be known as the singular matrix if the determinant of this matrix is equal to 0. In this section, we will learn about singular matrices, identifying a singular matrix, their properties, the difference between singular matrices and non-singular matrices, examples and many more things. What is Singular matrixIf the determinant of the given matrix is equal to 0, then the singular matrix must be a square matrix. In other words, a square matrix A will be known as singular if det A = 0. We have learned that we can find the inverse of a matrix A with the help of formula A-1 = (adj A) / (det A). Here det A is in the denominator, which is used to show the determinant of A. We know that if the determinant is equal to 0, in this case, we cannot define the fraction. Hence we cannot define the inverse of a matrix A, (A-1) if det A = 0. Because of this reason, there will not be any matrix B such that AB = BA = I, where I is used to indicate the identity matrix. From the above explanation, it is clear that a square matrix A will be known as singular if it contains following properties:

Identifying a Singular matrixWe have to check two conditions to identify whether the given matrix is a singular matrix, which is described as follows:
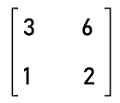
Now we will show some examples and determine whether the given matrix is a singular matrix. Suppose there is a matrix A where 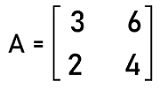
The order of this matrix is 2∗2. So this matrix is a square matrix. Now we will find the determinant of this matrix in the following way: |A| or det A = 3∗4 ' 6∗2 = 12 ' 12 = 0 The determinant of this matrix is 0. Hence this matrix is a square matrix. Steps to check the singular matrixIf we want to know whether the given matrix is singular or not, for this, we have to first calculate the determinant of the matrix. Here we will check it for the 2∗2 matrix and 3∗3 matrix one by one. For 2∗2 matrix:In the following steps, we will see how we can check whether the 3∗3 matrix is singular or not. Step 1: In this step, we will first check whether the given matrix is a square matrix. Step 2: The 2∗2 matrix is used to contain 4 elements (2 rows and 2 columns). So in this step, the determinant of matrix A will be ad-bc. It will be indicated by |A| or det A. Step 3: In this step, we will check the value of the determinant. If the determinant ad-bc = 0, in this case, matrix A will be known as the singular matrix. Otherwise we will check the next step. Step 4: If the determinant ad-bc ? 0, in this case, matrix A will be known as the non-singular matrix. Now we will understand all these steps with the help of an example. In this example, we have a 2∗2 matrix, A where 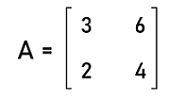
This matrix is a square matrix. So we will first calculate the determinant of the above matrix A like this: |A| or det A = 3∗4 ' 6∗2 |A| = 12 ' 12 |A| = 0 Here the determinant of A is equal to 0. Hence matrix A is a singular matrix. For 3∗3 matrix:In the following steps, we will see how we can check whether the 3∗3 matrix is singular or not. Step 1: In this step, we will first check whether the given matrix is a square matrix. Step 2: The 3∗3 matrix is used to contain 9 elements (3 rows and 3 columns). So in this step, the determinant of matrix A will be a1(b2c3 ' b3c2) ' a2(b1c3 ' b3c1) ' a3(b1c2 ' b2c1). It will be indicated by |A| or det A. Step 3: In this step, we will check the value of the determinant. If the determinant {a1(b2c3 ' b3c2) ' a2(b1c3 ' b3c1) ' a3(b1c2 ' b2c1) = 0}, in this case, the matrix A will be known as the singular matrix. Otherwise we will check the next step. Step 4: If the determinant {a1(b2c3 ' b3c2) ' a2(b1c3 ' b3c1) ' a3(b1c2 ' b2c1) ? 0}, in this case, the matrix A will be known as the non-singular matrix. Now we will understand all these steps with the help of an example. In this example, we have a 3∗3 matrix, A where 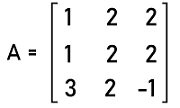
This matrix is a square matrix. So we will first calculate the determinant of the above matrix A like this: |A| or det A = 0 The determinant of A is equal to 0. This is because the first and second row of this matrix is equal. Hence matrix A is a singular matrix. Properties of Singular matrixHere we will define some properties of a singular matrix on the basis of its definitions. These properties are described as follows:
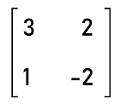
Singular matrix and Non-singular matrixAccording to the name, the non-singular matrix will not be singular. Thus, in case of the non-singular matrix, the determinant will be non-zero numbers. In other words, we can say that if det A ? 0, then the square matrix A will be known as the non-singular matrix. We can define the inverse of a matrix (A-1) in the non-singular matrix because there is always a multiplicative inverse in this matrix. In the following way, the difference between the singular matrix and the non-singular matrix can be shown: 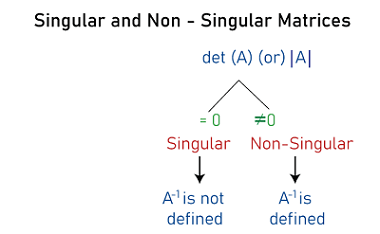
Theorem to Generate Singular matricesIn case of a singular matrix, there is one important theorem that is used to generate a singular matrix. According to this theorem, if there are two matrices A and B where A = [A]n∗k and B = [B]k∗n, then the multiplication of these matrices will be matrix AB, which contains the order n∗n, and it will always be singular. This theorem says that
With the help of this theorem, we can multiply two randomly generated matrices, which contain an order n∗k and k∗n and can generate a singular matrix. Here n > k. Examples of Non-singular matrixThere are a lot of examples of non-singular matrices, and some of them are described as follows: Example 1: In this example, we have two matrices, and we have to determine which matrix is a singular matrix. 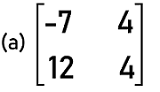
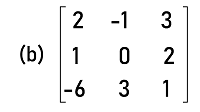
Solution: To find whether the given matrix is singular or not, we have to first determine the determinants of each given matrix one by one. 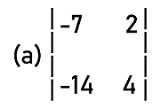
= -7∗4 ' 2∗(-14) = -28 + 28 = 0 The determinant of this matrix is 0. Hence this matrix is a square matrix. Now we will find the determinant of matrix (b). 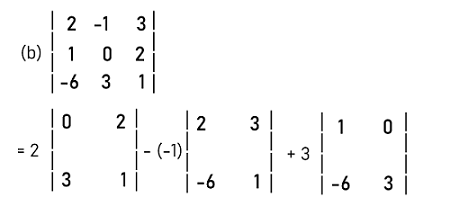
= 2(0-6) + 1(1+12) + 3(3-0) = -12 + 13 + 9 = 10 ≠ 0 So the determinant of this matrix is not equal to 0. Hence this matrix is not a singular matrix. Answer: (a) is a singular matrix, and (b) is a non-singular matrix. Example 2: In this example, we have a matrix A, and we have to determine whether this matrix is singular or not. The elements of matrix A are described as follows: 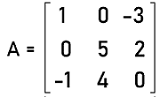
Solution: To find whether the given matrix is singular or not, we have to first determine the determinants of this matrix like this. det A = 1[(5∗0) ' (4∗2)] - 0[(0∗0) ' (2∗ -1)] + (-3)[(0∗4) ' (-1∗5)] |A| = (1 ∗ -8) ' 0 + (-3 ∗ 5) |A| = -8 ' 15 |A| = -23 ≠ 0 So the determinant of this matrix is not equal to 0. Hence this matrix is not a singular matrix. Example 3: In this example, we have a singular matrix A, and we have to determine the value of k. The elements of matrix A are described as follows: 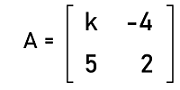
Solution: From the question, we know that matrix A is a singular matrix. So its determinant will be 0. So (2∗k) ' (-4∗5) = 0 2k + 20 = 0 2k = -20 k = -20 /2 k = -10 Hence the value of k will be -10 for A to be singular. Example 4: In this example, we have a singular matrix A, and we have to determine the value of x. The elements of matrix A are described as follows: 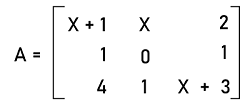
Solution: From the question, we know that matrix A is a singular matrix. So its determinant will be 0, i.e., 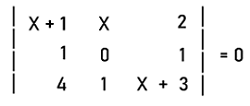
(x+1) (0-1) ' x(x+3-4) + 2(1-0) = 0 -x - 1 ' x2 + x + 2 = 0 -x2 + 1 = 0 x2 = 1 x = ±1 Hence x = 1 or -1 for A to be singular. Example 5: In this example, we have to find out whether the following system contains a unique solution or not. These systems are described as follows: 2x + y + 2z = 3 x + z = 5 4x + y + 4z = 7 Solution: From the question, we have three systems, and we can write these systems in the form of a matrix with the help of corresponding matrix equation, i.e., AX+B. After doing this, the coefficient matrix will become like this: 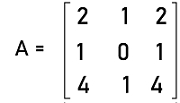
The system will have a unique solution if and only if the determinant of A is not equal to 0 (that means if A is non-singular). So we will determine the determinant of A like this: 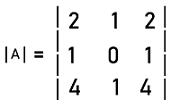
= 2(0-1) - 1(4-4) + 2(1-0) = -2 + 0 + 2 = 0 The determinant of matrix A is 0. So the system can either have no solution or have infinite solutions. Hence the system will NOT have a unique solution. Example 6: In this example, we have a singular matrix A, and we have to determine the value of b. The elements of matrix A are described as follows: 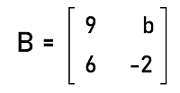
Solution: From the question, we know that matrix A is a singular matrix. So its determinant will be 0. So (9∗ -2) ' (6∗b) = 0 -18 ' 6b = 0 -6b = 18 b = 18 /-6 b = -3 Hence the value of b will be -3 for the given matrix A to be singular. Example 7: In this example, we have a matrix P, and we have to determine the inverse of this matrix. The elements of matrix P are described as follows: 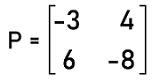
Solution: We can only find the inverse of this matrix if and only if the given matrix is not a singular matrix. That means the determinant of this matrix should not be equal to 0. From the given matrix, we have the following matrix like this: 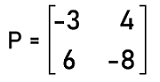
We can determine the inverse of matrix P with the help of following formula for the non-singular matrix: P-1 = adj P / |P| So to find it, we will determine the determinant of this matrix P like this: |P| = (-3 ∗ -8) ' (6∗4) |P| = 24 ' 24 |P| = 0 Since we can see that the determinant of matrix P is equal to 0. So it is a singular matrix, and the inverse of this matrix does not exist. |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share