Boolean Algebra:

A complemented distributive lattice is known as a Boolean Algebra. It is denoted by (B, ∧,∨,',0,1), where B is a set on which two binary operations ∧ (*) and ∨(+) and a unary operation (complement) are defined. Here 0 and 1 are two distinct elements of B.

Since (B,∧,∨) is a complemented distributive lattice, therefore each element of B has a unique complement.

Properties of Boolean Algebra:

1. Commutative Properties:

(i)a+b = b+a
(ii)a*b=b *a

2. Distributive Properties

(i) a+(b*c)=(a+b)*(a+c)
(ii)a*(b+c)=(a*b)+(a*c)

3. Identity Properties

(i) a+0=a
(ii) a *1=a

4. Complemented Laws:

(i) a+a'=1
(ii)a * a'=0

Sub-Algebra:

Consider a Boolean-Algebra (B, *, +,', 0,1) and let A ⊆ B. Then (A,*, +,', 0,1) is called a sub-algebra or Sub-Boolean Algebra of B if A itself is a Boolean Algebra i.e., A contains the elements 0 and 1 and is closed under the operations *, + and '.

Example: Consider the Boolean algebra D₇₀ whose Hasse diagram is shown in fig: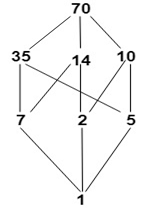

Clearly, A= {1, 7, 10, 70} and B = {1, 2, 35, 70} is a sub-algebra of D₇₀. Since both A and B are closed under operation ∧,∨and '.

Note: A subset of a Boolean Algebra can be a Boolean algebra, but it may or may not be sub-algebra as it may not close the operation on B.

Isomorphic-Boolean Algebras:

Two Boolean algebras B and B₁ are called isomorphic if there is a one to one correspondence f: B⟶B₁ which preserves the three operations +,* and ' for any elements a, b in B i.e.,
f (a+b)=f(a)+f(b)
f (a*b)=f(a)*f(b) and f(a')=f(a)'.

Example: The following are two distinct Boolean algebras with two elements which are isomorphic.

1.The first one is a Boolean Algebra that is derived from a power set P(S) under ⊆ (set inclusion),i.e., let S = {a}, then B = {P(S), ∪,∩,'} is a Boolean algebra with two elements P(S) = {∅,{a}}.

2. The second one is a Boolean algebra {B, ∨,∧,'} with two elements 1 and p {here p is a prime number} under operation divides i.e., let B = {1, p}. So, we have 1 ∧ p = 1 and 1 ∨ p = p also 1'=p and p'=1.

The table shows all the basic properties of a Boolean algebra (B, *, +, ', 0, 1) for any elements a, b, c belongs to B. The greatest and least elements of B are denoted by 1 and 0 respectively.

1. a ≤b iff a+b=b 2. a ≤b iff a * b = a
3. Idempotent Laws    4. Commutative Property
(i)a+b=a    (i)a+b=b+a
(ii) a * a = a (ii)a*b=b*a
5. Associative Property 6. Absorption Laws
(i)a+(b+c)=(a+b)+c (i)a+(a*b)=a
(ii)a*(b*c)=(a*b)*c (ii)a*(a+b)=a
7. Identity Laws    8. Null Laws
(i) a+0=a (i)a*0=0
(ii) a*1=a (ii)a+1=1
9. Distributive Laws 10. Complement Laws
(i)a*(b+c)=(a*b)+(a*c) (i)0'=1
(ii) a+(b*c) = (a+b)*(a+c) (ii)1'=0
(iii)a+a'=1
(iv)a*a'=0
11. Involution Law    12.De Morgan's Laws
(a')'=a (i)(a *b)'=(a' +b')
      (ii) (a+b)'=(a' *b')

Note:
1. 0 ≤ a ≤ 1 for every a ∈ B.
2. Every element b has a unique complement b'.

Boolean Functions:

Consider the Boolean algebra (B, ∨,∧,',0,1). A function from A''to A is called a Boolean Function if a Boolean Expression of n variables can specify it.

For the two-valued Boolean algebra, any function from [0, 1]ⁿ to [0, 1] is a Boolean function.

Example1: The table shows a function f from {0, 1}³ to {0, 1}