Particular Solution(a) Homogeneous Linear Difference Equations and Particular Solution:We can find the particular solution of the difference equation when the equation is of homogeneous linear type by putting the values of the initial conditions in the homogeneous solutions. Example1: Solve the difference equation 2ar-5ar-1+2ar-2=0 and find particular solutions such that a0=0 and a1=1. Solution: The characteristics equation is 2s2-5s+2=0 Therefore, the homogeneous solution of the equation is given by ar(h)= C1 Putting r=0 and r=1 in equation (i), we get Solving eq (a) and (b), we have Hence, the particular solution is Example2: Solve the difference equation ar-4ar-1+4ar-2=0 and find particular solutions such that a0=0 and a1=6. Solution: The characteristics equation is Therefore, the homogeneous solution of the equation is given by Putting r = 0 and r = 1 in equation (i), we get Hence, the particular solution is Example3: Solve the difference equation 9ar-6ar-1+ar-2=0 satisfying the conditions a0=0 and a1=2. Solution: The characteristics equation is 9s2-6s+1=0 or (3s-1)2=0s = 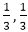
Therefore, the homogeneous solution of the equation is given by Putting r = 0 and r = 1 in equation (i), we get Hence, the particular solution is (b) Non-Homogeneous Linear Difference Equations and Particular Solution:There are two methods to find the particular solution of a non-homogeneous linear difference equation. These are as follows:
1. Undetermined Coefficients Method: This method is used to find a particular solution of non-homogeneous linear difference equations, whose R.H.S term R (n) consist of terms of special forms. In this method, firstly we assume the general form of the particular solutions according to the type of R (n) containing some unknown constant coefficients, which have to be determined. Then according to the difference equation, we will determine the exact solution. The general form of a particular solution to be assumed for the special forms of R (n), to find the exact solution is shown in the table.
Example1: Find the particular solution of the difference equation ar+2-3ar+1+2ar=Zr ........equation (i) Where Z is some constant. Solution: The general form of solution is = A. Zr Now putting this solution on L.H.S of equation (i), we get Equating equation (ii) with R.H.S of equation (i), we get Therefore, the particular solution is Example2: Find the particular solution of the difference equation ar+2-5ar+1+6ar=5r .............equation (i) Solution: Let us assume the general form of the solution= A. 5r. Now to find the value of A, put this solution on L.H.S of the equation (i), then this becomes Equating equation (ii) to R.H.S of equation (i), we get Therefore, the particular solution of the difference equation is = Example3: Find the particular solution of the difference equation ar+ 2+ar+1+ar=r.2r..........equation (i) Solution: Let us assume the general form of the solution = (A0+A1r). 2^r Now, put these solutions in the L.H.S of the equation (i), we get Equating equation (ii) with R.H.S of equation (i), we get Therefore, the particular solution is 2. E and ∆ operator Method: Definition of Operator E: The operator of E on f(x) means that give an increment to the value of x in the function. The operation of E is, put (x+h) in the function wherever there is x. Here h is increment quantity. So Ef(x) = f(x+h) Here, E is operated on f(x), therefore, E is a symbol known as shift operator. Definition of Operator∆: The operation ∆ is an operation of two steps. Firstly, x in the function is incremented by a constant and then former is subtracted from the later i.e., Theorem1: Prove that E ≅1+∆. Proof: The operation of ∆ on f(x) is of two steps. First, increment the value of x in the function. So, whenever, there is x in f(x) put x+h (here h is constant increment), which means operation of E on f(x) i.e., Second, subtract the original function from the value obtained in the first step, hence So, the operation of ∆ on f(x) is equivalent to the operation of (E-1) on f(x). Therefore, we have Theorem2: Show that En f(x)=f(x+nh). Proof: We know that E f(x) =f (x+h) Now En f(x)=E.E.E.E.........n times f(x) Theorem3: Show that E Cf(x) = CE f(x) Proof: We know that E C f(x) = C f(x+h) = CE f(x+h). Hence Proved. There is no effect of the operation of E on any constant. Therefore, the operation of E on any constant will be equal to constant itself. By E and ∆ operator method, we will find the solution of Equation (i) can be written as So P (E) yn=R (n) To find the particular solution of (ii) for different forms of R (n), we have the following cases. Case1: When R (n) is some constant A. We know that, the operation of E on any constant will be equal to the constant itself i.e., P (1) is obtained by putting E = 1 in P (E). Case2: When R (n) is of the form A. Zn, where A and Z are constants We have, P (E) (A. Zn)={C0 Er+C1 Er-1+⋯+ Cn} (A.Zn) To get, P (Z) put E=Z in P (E) Therefore, Thus, yn= If A = 1, then yn= When P (Z) = 0 then for equation (i) (E-Z) yn= A. Zn For this, the particular solution becomes A. (ii) (E-Z)2 yn= A. Zn For this, the particular solution becomes (iii) (E-Z)3 yn= A. Zn For this, the particular solution becomes Case3: When R (n) be a polynomial of degree m is n. We know that E≅1+∆ 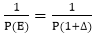
Which can be expanded in ascending power of ∆ as far as upto ∆m ⇒ All other higher terms will be zero because R (n) is a polynomial of degree m. Thus, the particular solution of equation (i), in this case will be yn=b0 R(n)+b1 ∆ R(n)+⋯.+bm ∆m R(n). Case4: When R (n) is of the form R(n).Zn,where R(n) is a polynomial of degree m and Z is some constant We have Er[Zn R(n)]=Zr+n R (n+r)=Zr.Zn.Er.R(n)=Zn (ZE)rR(n) Similarly, we have Thus, the particular solution of equation (i), in this case will be Example1: Find the particular solution of the difference equation Solution: The above equation can be written as The particular solution is given by Put E=1, in the equation. The particular solution is ar=12 Example2: Find the particular solution of the difference equation ar-4ar-1+4ar-2=2r. Solution: The above equation can be written as Therefore, P (E) = E2-4E+4 = (E-2)2 Thus, the particular solution is given by 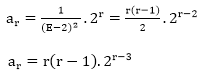
Next TopicTotal Solution
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





 and 2.
and 2.
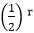 +C2 .2r..........equation (i)
+C2 .2r..........equation (i)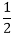 C1+2C2=1...........equation.(b)
C1+2C2=1...........equation.(b)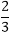 and C2=
and C2=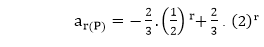
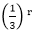 ..........equation (i)
..........equation (i)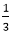 =2. ∴C1+C2=6⇒C2=6
=2. ∴C1+C2=6⇒C2=6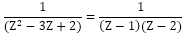 (Z≠1, Z≠2)
(Z≠1, Z≠2)
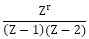
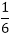
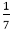
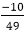
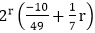
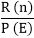 ................equation (ii)
................equation (ii)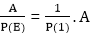
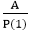 ,P(1)≠0
,P(1)≠0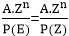 , provided P (Z) ≠ 0
, provided P (Z) ≠ 0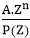 , P (Z) ≠ 0
, P (Z) ≠ 0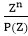
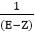 Zn=A. n Zn-1
Zn=A. n Zn-1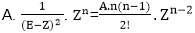
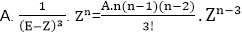 and so on.
and so on.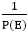 .R(n)=( b0+b1 ∆+b2 ∆+⋯.+bm ∆m+⋯).R(n)
.R(n)=( b0+b1 ∆+b2 ∆+⋯.+bm ∆m+⋯).R(n)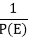 [Zn R(n)]=Zn
[Zn R(n)]=Zn 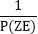 .(R(n))= Zn [P(Z+Z∆)]-1.R(n)
.(R(n))= Zn [P(Z+Z∆)]-1.R(n)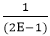 .12
.12




