Square matrix in discrete mathematics

In the field of discrete mathematics, the most commonly used element is the matrix. A matrix is used to contain the rectangular array of numbers, and all these numbers, expressions, or symbols will be arranged in the form of rows and columns. The rows elements are arranged in the form of a horizontal manner, and the column elements are arranged in the form of a vertical manner. With the help of a number of rows and columns, we can determine the order of matrix. If there is a matrix that contains 3 rows and 2 columns, then the order of this matrix will be 3∗2. In the same way, if there is a matrix that contains an equal number of rows and columns, then this type of matrix will be a square matrix.

In the field of matrix, there is an important format which is known as the square matrix. This type of matrix is used to contain the perfect square number of elements. This matrix contains an equal number of rows and columns. That's why the order of this matrix will always be n∗n. We can apply various kinds of matrix operations on the square matrix, such as adjoint, inverse, transpose, determinant, and mathematical operations of matrices. In this section, we are going to learn about the square matrix, its transpose, determinant, inverse, matrix operations, examples of square matrix, and many more things.

What is Square matrix

A matrix will be known as a square matrix if there is an equal number of rows and columns in the matrix. The order of a square matrix will be in the form n∗n. If we do the addition or multiplication of two square matrices, then the resultant matrix will be in the same order. Hence we can say that the number of elements in this process will always be a perfect square number. Suppose we are trying to solve a problem related to quadratic equations in two variables. In this case, we can easily do this with the help square matrix because this matrix has a special application for this. The typical form of a square matrix is shown below: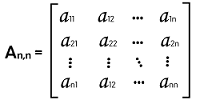

Examples of a Square matrix

There are various examples of a square matrix, and some of them are described as follows:

Example 1: In this example, we have a matrix X, which is described as follows: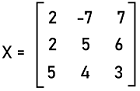

In the above example, there is a matrix that contains an equal number of rows and columns, which is 3. We can say that the order of matrix is 3∗3. Hence matrix X is a square matrix. Here if we want to determine the determinant of 3∗3 square matrix, then we can also do that.

Example 2: In this example, we have another matrix Y, which is described as follows: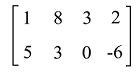

In the above example, there is a matrix in which the number of rows is 2, and the number of columns is 4. Since this matrix does not contain an equal number of rows and columns. Hence matrix Y is not a square matrix.

Examples of Square matrix on the basis of order

Here we will show the square matrices with different orders, which are described as follows:

Square matrix of order 2

The general form of a square matrix with order 2∗2 is described as follows: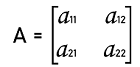

In this image, we can see a matrix of order 2. This matrix contains 4 elements, which are arranged in the form of 2 rows and 2 columns. Hence this matrix is a square matrix.

For example: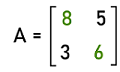

In the above example, there is a 2∗2 square matrix A. The diagonal of this matrix is 8, 6, which is the principal diagonal. Here 8 and 6 are also known as the diagonal elements.

Square matrix of order 3

The general form of a square matrix with order 3∗3 is described as follows: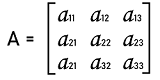

In this image, we can see a matrix of order 3. This matrix contains 9 elements, which are arranged in the form of 3 rows and 3 columns. Hence this matrix is a square matrix.

For example: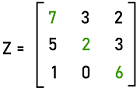

In the above example, there is a 3∗3 square matrix A. The diagonal of this matrix is 7, 2, 6, which is the principal diagonal. Here 7, 2, and 6 are also known as the diagonal elements.

Square matrix of order 4

The general form of a square matrix with order 4∗4 is described as follows: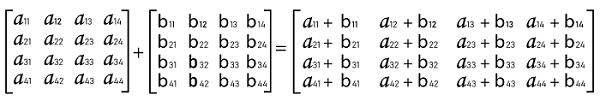

In this image, we can see a matrix of order 4. This matrix contains 16 elements, which are arranged in the form of 4 rows and 4 columns. Hence this matrix is a square matrix.

For example: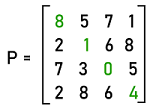

In the above example, there is a 4∗4 square matrix A. The diagonal of this matrix are 8, 1, 0, 4, which is the principal diagonal. Here 8, 1, 0, and 4 are also known as the diagonal elements.

Transpose of a square matrix

For a given matrix if the values of rows are changed into columns, and the values of columns are changed into rows, then that type of matrix will be known as the transpose of that matrix. Generally, when we change the matrix into the transpose matrix, then the order of the matrix will also be changed. If there is a matrix that contains an order m∗n, then the transpose of that matrix will be in the order n∗m. In case of a square matrix, the given matrix and the transpose matrix both have the same order. The example of transpose of a square matrix is described as follows: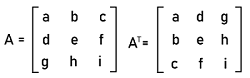

There are two important terms that are related to the concept of transpose a matrix, i.e., symmetric matrix and skew-symmetric matrix. The symmetric matrix can be described as a matrix in which the given square matrix and the transpose of that matrix are similar to each other. The skew-symmetric matrix can be described as a matrix in which the transpose of a given square matrix and the negation of that matrix are similar to each other. The syntax of a symmetric matrix and a skew-symmetric matrix is described as follows:

Symmetric matrix: AT = A
Skew-symmetric matrix: AT = -A

Determinant of a square matrix

With the help of a formula, we can very easily calculate the determinant of a matrix that contains an order 2∗2. If we do the subtraction of multiplication of diagonal elements of the matrix, we can get the determinant of a matrix of order 2∗2. Suppose there is matrix, A, which contains an order 2∗2. The determinant of this matrix, A can be calculated in the following way: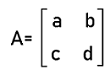

Inverse of Square matrix

In the process of inverse of a square matrix, one matrix will be divided by another matrix. We can only determine the inverse of a square matrix with the help of finding some things. We need to determine the determinant of the matrix first to determine the inverse of a square matrix. After that, we will calculate the adjoint of the square matrix. Finally, we will divide the adjoint and determinant of the square matrix so that we can get the inverse of that matrix.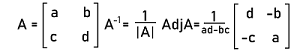

While learning the inverse of a square matrix, there is an important term that we should know, i.e., an orthogonal matrix. If the transpose of a square matrix and its inverse are similar to each other, then this type of square matrix will be known as the orthogonal matrix. With the help of following expression, we can indicate the orthogonal matrix:

Orthogonal matrix: AT = A-1

Matrix operation on Square matrix

In case of a square matrix, there are three types of mathematical operations that can be performed, i.e., multiplication, addition, and subtraction.

Addition and Subtraction of Square matrices

In case of addition or subtraction of two square matrices, we will get the resultant matrix by adding or subtracting the corresponding elements of the matrices. The matrix addition contains an important point, i.e., it follows the commutative property (A + B = B + A). Suppose there are two square matrices, A and B, which contain an order 3∗3. The addition process of these matrices is described as follows: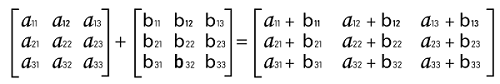

The example of addition of square matrices is described as follows: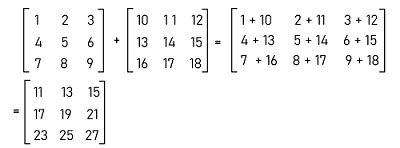

In this example, we have easily performed the addition of square matrices. Here we add the first matrix's value to the corresponding values of the second matrix.

Suppose there are two square matrices, A and B, which contain an order 2∗2. The process of addition and subtraction of these matrices is described as follows: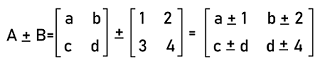

Multiplication of Square matrices

It is very easy to do the matrix scalar multiplication. If we want to do the multiplication of a square matrix by a constant matrix, in this case, we have to multiply each element of the matrix with the constant.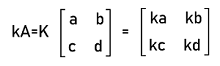

There is a sequence of steps that should be followed to multiply the two square matrices. Suppose there are two square matrices that contain an order 2∗2. In the first matrix, we will assume the row elements, and in the second matrix, we will consider the column elements. There are two 2∗2 square matrices, then the multiplication of these matrices is described as follows: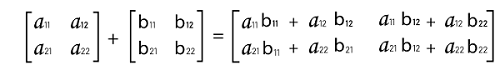

While doing the matrix multiplication, there is some sequence of calculations that will be followed. We will understand those steps with the help of an example, which is described as follows:

Important terms used in Square matrix

Here we will see some important terms which are used while learning the concept of a square matrix. These terms will be helpful to deeply understand the concept of a square matrix, which are described as follows:

Order of a matrix: The order of a matrix can be calculated by the multiplication of rows and columns. In case of a square matrix, there will be an equal number of rows and columns in the matrix. This is because the order of square matrix will be n∗n.

Trace of a matrix: The trace of a matrix can be calculated by adding the diagonal elements of a square matrix.

Symmetric matrix: A matrix will be known as a symmetric matrix if the given matrix and the transpose of that matrix are similar to each other.

Orthogonal matrix: If the transpose of a matrix and the inverse of that matrix are similar to each other, in this case, the matrix will be an orthogonal matrix.

Identity matrix: If there is a square matrix in which all the diagonal elements are equal to 1 and all the other elements except diagonal elements are equal to 0, in this case, the matrix will be an identity matrix.

Skew-symmetric matrix: If the negation of a matrix and the transpose of that matrix are similar to each other, in this case, the matrix will be a skew-symmetric matrix.

Scalar matrix: If there is a square matrix that contains all the same numbers or if all the diagonal elements and all the other elements of the given matrix are 0, in this case, the matrix will be a scalar matrix.

Properties of Square matrix

There are a lot of properties of a square matrix, and some of them are described as follows:

• For a square matrix, the number of rows and the number of columns must be similar to each other.
• If there is a square matrix, then the addition of all diagonal elements of this matrix will be known as the trace of a matrix.
• If there is a square matrix and all the diagonal elements of this matrix are 1, in this case, this matrix will be known as the identity matrix.
• There can be different kinds of operations that can be performed on the square matrix, like inverse operation.
• In case of a square matrix only, we will be able to calculate the determinant value.
• In case of a square matrix, the original matrix and the transpose matrix both have the same order.