Hasse DiagramsIt is a useful tool, which completely describes the associated partial order. Therefore, it is also called an ordering diagram. It is very easy to convert a directed graph of a relation on a set A to an equivalent Hasse diagram. Therefore, while drawing a Hasse diagram following points must be remembered.
The Hasse diagram is much simpler than the directed graph of the partial order. Example: Consider the set A = {4, 5, 6, 7}. Let R be the relation ≤ on A. Draw the directed graph and the Hasse diagram of R. Solution: The relation ≤ on the set A is given by R = {{4, 5}, {4, 6}, {4, 7}, {5, 6}, {5, 7}, {6, 7}, {4, 4}, {5, 5}, {6, 6}, {7, 7}} The directed graph of the relation R is as shown in fig: 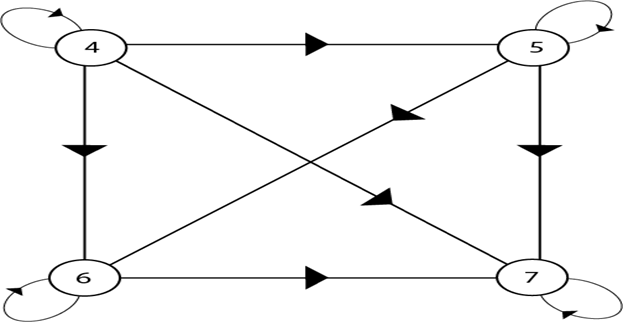
To draw the Hasse diagram of partial order, apply the following points:
The Hasse diagram is as shown in fig: 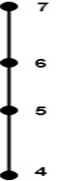 Upper Bound: Consider B be a subset of a partially ordered set A. An element x ∈ A is called an upper bound of B if y ≤ x for every y ∈ B. Lower Bound: Consider B be a subset of a partially ordered set A. An element z ∈ A is called a lower bound of B if z ≤ x for every x ∈ B. Example: Consider the poset A = {a, b, c, d, e, f, g} be ordered shown in fig. Also let B = {c, d, e}. Determine the upper and lower bound of B. 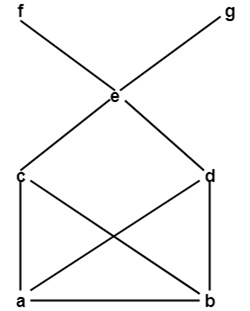 Solution: The upper bound of B is e, f, and g because every element of B is '≤' e, f, and g. The lower bounds of B are a and b because a and b are '≤' every elements of B. Least Upper Bound (SUPREMUM):Let A be a subset of a partially ordered set S. An element M in S is called an upper bound of A if M succeeds every element of A, i.e. if, for every x in A, we have x <=M If an upper bound of A precedes every other upper bound of A, then it is called the supremum of A and is denoted by Sup (A) Greatest Lower Bound (INFIMUM):An element m in a poset S is called a lower bound of a subset A of S if m precedes every element of A, i.e. if, for every y in A, we have m <=y If a lower bound of A succeeds every other lower bound of A, then it is called the infimum of A and is denoted by Inf (A) Example: Determine the least upper bound and greatest lower bound of B = {a, b, c} if they exist, of the poset whose Hasse diagram is shown in fig: 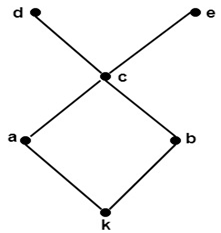 Solution: The least upper bound is c. The greatest lower bound is k.
Next TopicLattices
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









