Matrix in Discrete mathematics

A matrix can be described as a rectangular array of numbers. A matrix that has m numbers of rows and n number of columns, then it will be known as an m∗n matrix. If there is more than one matrix, then it will call matrices.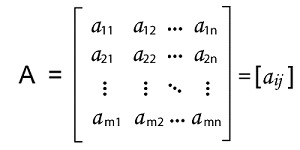

We can indicate the matrix with the help of capital letters. The array of numbers is enclosed with the help of parenthesis or brackets.

For example: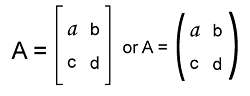

We cannot write a matrix by using a straight line instead of brackets. This is because the matrix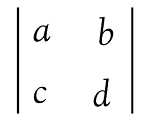

is used to show a special meaning in the field of linear algebra. If we want to represent the elements, then we can use a shorthand notation, i.e., A = [a_ij]. In this notation, the first subscript i is used to indicate the row number, and the subscript j is used to indicate the column number of entry a_ij. Thus, if we are trying to write a₂₃, then it will refer to the element in the 2^nd row and 3^rd column. With the help of this notation, we cannot show the dimensions of matrix. From this notation, we can say that two m∗n matrices A = [a_ij] and B = [b_ij] will be equal iff a_ij = b_ij for all i and j.

For example: In this example, we have a 2∗3 matrix.

If there is a matrix that has the same number of rows and columns, then that matrix will be known as a square matrix. If two given matrices contain the same number of rows and columns, and their corresponding entries in every position are the same, in this case, these matrices will be equal.

For example: In this example, we have a 3∗2 matrix, which is described as follows: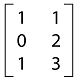

Suppose there is a matrix A where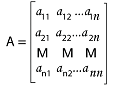

In this matrix, the i^th row of matrix A will be 1∗n matrix [a_i1, a_i2, ...., a_in], and the j^th column of matrix A will be n∗1 matrix, which is described as follows: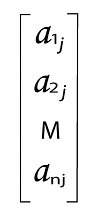

The (i, j)th element or entry of A can be described as an element a_ij which says that the number in the i^th row and j^th column of A.

There is a convenient method in which we can simply express the matrix A, i.e., A = [a_ij]. This equation shows that there is a matrix A, which has (i, j)th element equal to a_ij.

Some Important points

There are some terms that we should know when we learn about matrix, which are described as follows:

Element:

Each and every value in a matrix will be known as the element, whether it is a number or a constant.

Dimension:

The dimension of a matrix can be described as the number of rows by the number of columns. With the help of dimension, we can name the matrix.

For example: In this example, we must determine each matrix's dimension.

In this matrix, there are 3 number of rows and 2 number of columns. So this matrix has a 3∗2 dimension.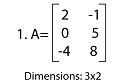

In this matrix, there are 2 number of rows and 4 number of columns. So this matrix has a 2∗4 dimension.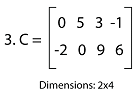

In this matrix, there are 4 number of rows and 1 number of column. So this matrix has a 4∗1 dimension.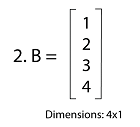

Row matrix

If there is a matrix that has only one row, then it will be a row matrix. This matrix is indicated by [1∗n]. The one-row matrix is described as follows:

A[a1 a2 a3, ...., an] = {aj}

Column matrix

If there is a matrix that has only one column, then it will be a column matrix. This matrix is indicated by [m∗1]. The one-column matrix is described as follows: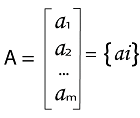

Square matrix

A matrix will be known as a square matrix if there is an equal number of rows and an equal number of columns. The (n∗n) will be a square matrix.

For example: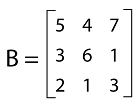

Equal matrix

Suppose there are two matrices A = [a_ij] and B = [b_ij]. These matrices will be known as an equal matrix (A = B) if each element of A is same as the corresponding element of B, i.e., a_ij = b_ij for 1 ≤ I ≤ m, 1 ≤ j ≤ n.

For example: Suppose there are two equal matrices A and B (A = B) where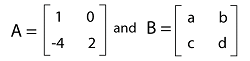

Now have to determine a, b, c, and d.

Solution: From the question, we have A = B. So

A = 1
B = 0
C = -4
D = 2

Properties of Matrix

1. (AB)^-1 = B^-1 A^-1
2. (AT)^T = A and (λA)^T = λA^T
3. (A + B)^T = A^T + B^T
4. (A B)^T = B^T A^T

Matrix Operations

There are various operations that can be performed on the matrix, which are described as follows:

1. Matrix addition
2. Matrix subtraction
3. Matrix equality
4. Matrix multiplication

Now we will explain them one by one.

Matrix Addition

Suppose there are two matrices, A and B, where A = [a_ij] and B = [b_ij]. Here i and j are used to indicate any value. This matrix is in the form m∗n. With the help of symbol A+B, we can indicate the sum of A and B. If A = a_ij and B = b_ij, then the addition of A and B can be described as follows:

A + B = aij + bij

Suppose there are two matrices, A and B, which contain the following element: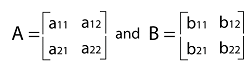

The addition of A and B will be C, which contains the following matrix: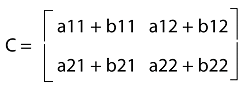

For example: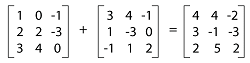

Properties

There are some properties that are contained by matrix addition, which are described as follows:

Suppose matrix A, B, and C are conformable. Then

It will contain the commutative law, which contains the following relation:

A+B = B+A

It will contain the associative law, which contains the following relation:

A+(B+C) = (A+B)+C

It will contain the distributive law, which contains the following relation:

λ(A+B) = λA + λB, where λ is used to indicate a scalar.

Matrix Subtraction

In the subtraction process, we will subtract elements of same position in the given matrices. If there are two matrices, A and B, which have the same dimension or have the same order, only then we can subtract them. If two given matrices have two different orders, then we cannot perform the subtraction operation on them. With the help of symbol A-B, we can indicate the subtraction of A and B. If A = a_ij and B = b_ij, then the subtraction of A and B can be described as follows:

A - B = aij - bij

Here i and j can have any value.

Example 1: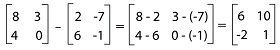

Example 2: Suppose there are two matrices, A and B. Now have to calculate the sum and subtraction of two given matrices. Matrix A and Matrix B are described as follows: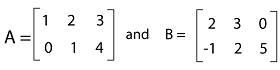

Solution: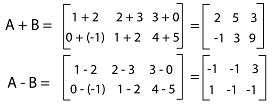

Matrix equality

Suppose there are two matrices, A and B. These two matrices will be equal if there are the same number of rows and columns in the matrices, and every element at each position in A will have the same element at the corresponding position in B. In this type of matrix, matrices will have the same corresponding entries.

For example:

Matrix Multiplication:

If there are two matrices, A and B, where A has an m∗k matrix and B has a k∗n matrix. We can perform the multiplication operation of two given matrices only if the number of columns in 1^st matrix and the number of rows in 2^nd matrix are similar to each other. With the help of symbol A∗B, we can indicate the multiplication of A and B. In the multiplication process, we will multiply rows by columns. If there is a matrix A, which is an a∗b matrix, and another matrix B which is a b∗c matrix, then the multiplication of A and B can be described as follows:

C = AB

Here matrix C is used to indicate the resultant matrix.

Suppose matrix C contains elements x and y, then it will be defined as

Cxy = Ax1By1 + Ax2By2 + .... + AxbBby = ∑bk=1 AxkBky

For x = 1....a and y = 1....c

In this process, the addition of multiplication of the ith row of matrix A to the corresponding element of jth column of matrix B will be equal to the product of A∗B matrix with its (i, j)th entry.

For example: In this example, we have two matrices, which are described as follows: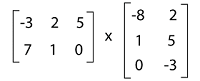

The dimension of first matrix is 2∗3, and the dimension of the second matrix is 3∗2. So we can see that number of rows in the 1^st matrix is equal to the number of column in the 2^nd matrix. Similarly, the number of columns in the 1^st matrix is equal to the number of rows in the 2^nd matrix. So we can multiply the given matrices.

Example of matrix multiplication

There are various examples of matrix multiplication, and some of them are described as follows:

Example 1: In this example, we have two matrices, A and B where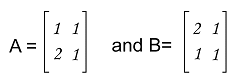

Now we have to show whether AB is equal to BA or not.

Solution: By multiplying AB, we will get: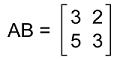

By multiplying BA, we will get: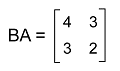

So we can see that AB ≠ BA.

This is because matrix multiplication is not commutative.

Example 2: In this example, we have three matrices A, B, and C where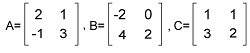

Now have to determine A(B+C) and AB+AC.

Solution: First we will solve A(B+C) like this: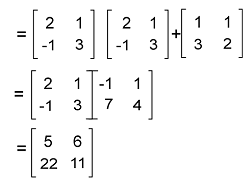

Now we will solve AB+AC like this: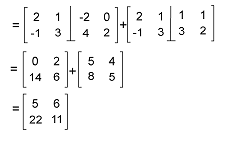

Example 3: In this example, we have two matrices, and we have to determine C = AB. The matrices of A and B are show below: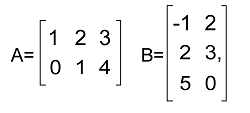

Solution: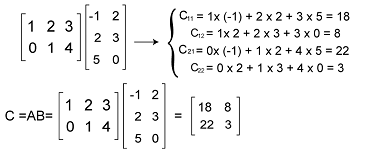

Property of Matrix multiplication

There are some properties that are contained by matrix multiplication, which are described as follows:

Suppose matrix A, B, and C are conformable. Then

A(B+C)= AB + AC
(A+B)C = AC + BC
A(BC) = (AB)C

Identity matrix

An identity matrix can be described as a matrix in which all the diagonal elements of the given matrix are 1. The identity matrix is indicated by the symbol I.

For example: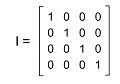

A∗I = A

The identity matrix of order n can be described as an n∗n matrix I_n = [ð_ij], where ð_ij= 1 if i = j and ð_ij = 0 if i ≠j. Hence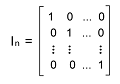

Ar = A ∗ A ∗ A ... ∗ A (r times)
A0 = In

Example of identity matrix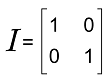

This is a 2∗2 identity matrix because the diagonal element of this matrix 1.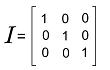

This is a 3∗3 identity matrix because the diagonal element of this matrix is also 1.

Transposes of a matrix

Suppose there is a matrix A = [a_ij] which is an m∗n matrix. We can get the transpose of matrix A with the help of interchanging the rows and columns of A. With the help of symbol A' or A^t, we can indicate the transpose of matrix A. In other words, we can say that if A^t = [b_ij], then b_ij = a_ij for i = 1, 2, 3, ...., n and j = 1, 2, 3, ... , m.

So transpose of a matrix can be described as a new matrix that can be formed by interchanging the rows and columns.

Thus,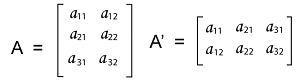

A is symmetric if and only if A = A'.

For example: Suppose there is a matrix A where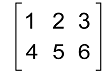

Now we have to determine the transpose of this matrix.

Solution: The transpose of this matrix will get by interchanging the rows and columns like this: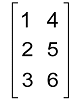

Null matrix

A matrix will be known as a null matrix if there is a square matrix in which all the elements are zero. The example of a null matrix is described as follows:

Symmetric matrix

Suppose there is a square matrix A. This matrix will be known as the symmetric matrix if A = A^t.

Thus if a_ij = a_ij for all i and j, then A = [a_ij] will be symmetric where 1 ≤ i ≤ n and 1 ≤ j ≤ n.

Theorems:

There are some theorems in case of a symmetric matrix, which are described as follows:

• If there are two matrices A and B which has n∗n symmetric matrices, then (AB)' = BA.
• If there are two matrices A and B which has n∗n symmetric matrices, then (A+B)' = B+A.
• If there is a matrix C that has any n∗n matrix, then B = C'C will be symmetric.

For example: The following matrix is a symmetric matrix: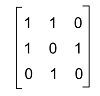

Zero-one Matrices

A matrix will be known as the zero-one matrix if entries of that matrix are either 0 or 1. We often used this matrix in the form of a table so that we could represent the discrete structures. If we want to define the Boolean operations, we can define their entries in the form of zero one matrix like this:

b1 ∧ b2 = 1 if b1 = b2 = 1

0 Otherwise

b1 ∨ b2 = 1 if b1 = 1 or b2 = 1

0 otherwise

Now we will define Boolean operations on entries in zero-one matrices in table form like this:

Suppose there are two matrices, A and B, which are the m∗n zero one matrices where A = [a_ij] and B = [b_ij]. The Join of A and B will be zero one matrix with (i, j)th entry a_ij ∨ b_ij. With the help of symbol A ∨ B, we can indicate the join of A and B. The meet of A and B will be zero one matrix with (i, j)th entry a_ij ∧ b_ij. With the help of symbol A ∧ B, we can indicate the meet of A and B.

For example: Suppose there are two matrices, A and B where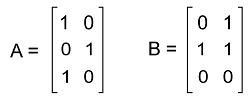

The Join of these matrices is described as follows: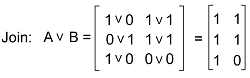

The meet of these matrices are described as follows: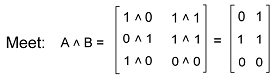

Suppose there are two matrices, A and B, where A = [a_ij], which is an m∗k zero one matrix, and B = [b_ij], which is a k∗n zero one matrix. The Boolean product of A and B will be an m∗n matrix that has (i, j)th entry [c_ij] in the following way:

cij = (ai1 ∧ b1j) ∨ (ai2 ∧ b2j) ∨ (ai3 ∧ b3j) ∨ ..... ∨ (aik ∧ bkj)

With the help of symbol AoB, we can indicate the Boolean product of A and B.

Basically, the working of matrices multiplication and Boolean multiplication both are similar, but in Boolean multiplication, we use ∧ instead of product and ∨ instead of sum.

Example 1: Suppose there are two matrices, A and B where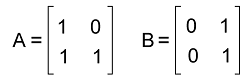

The Boolean multiplication of A and B is described as follows: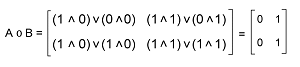

Example 2: Suppose there are two matrices, A and B where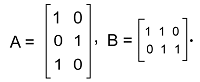

Now we have to determine the Boolean product of these matrices.

Solution: The product of A and B is described as follows: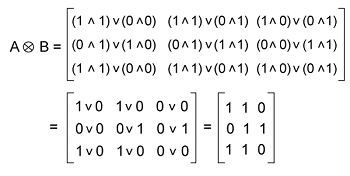

Suppose there is a zero one matrix A and r is a positive integer.

The r^th Boolean power of A is known as the Boolean product of r factors of A. With the help of symbol A^[r], we can indicate the Boolean power of A.

A^[0] = I_n,

A^[r] = AoAo .... oA (r times the letter A)