Representation of GraphsThere are two principal ways to represent a graph G with the matrix, i.e., adjacency matrix and incidence matrix representation. (a)Representation of the Undirected Graph:1. Adjacency Matrix Representation: If an Undirected Graph G consists of n vertices then the adjacency matrix of a graph is an n x n matrix A = [aij] and defined by 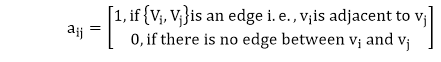
If there exists an edge between vertex vi and vj, where i is a row and j is a column then the value of aij=1. If there is no edge between vertex vi and vj, then value of aij=0. Example: Find the adjacency matrix MA of graph G shown in Fig: 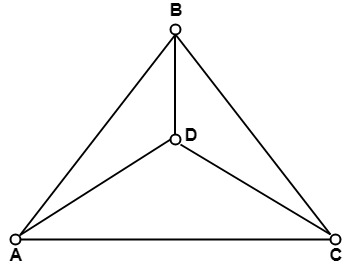
Solution: Since graph G consist of four vertices. Therefore, the adjacency matrix wills a 4 x 4 matrix. The adjacency matrix is as follows in fig: 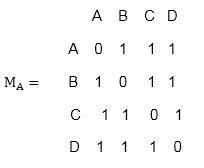
2. Incidence Matrix Representation: If an Undirected Graph G consists of n vertices and m edges, then the incidence matrix is an n x m matrix C = [cij] and defined by 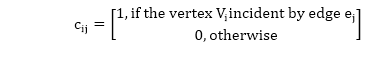
There is a row for every vertex and a column for every edge in the incident matrix. The number of ones in an incidence matrix of the undirected graph (without loops) is equal to the sum of the degrees of all the vertices in a graph. Example: Consider the undirected graph G as shown in fig. Find its incidence matrix MI. 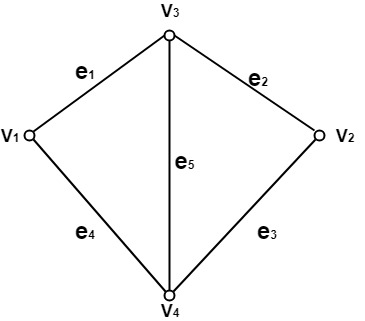
Solution: The undirected graph consists of four vertices and five edges. Therefore, the incidence matrix is an 4 x 5 matrix, which is shown in Fig: 
(b)Representation of Directed Graph:1. Adjacency Matrix Representation: If a directed graph G consists of n vertices then the adjacency matrix of a graph is an n x n matrix A = [aij] and defined by 
If there exists an edge between vertex Vi and Vj, with Vi as initial vertex and Vj as a final vertex, then the value of aij=1. If there is no edge between vertex Vi and Vj, then the value of aij=0. The number of ones in the adjacency matrix of a directed graph is equal to the number of edges. Example: Consider the directed graph shown in fig. Determine its adjacency matrix MA. 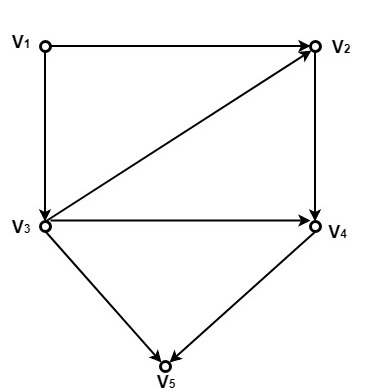
Solution: Since the directed graph G consists of five vertices. Therefore, the adjacency matrix will be a 5 x 5 matrix. The adjacency matrix of the directed graphs is as follows: 
2. Incidence Matrix Representation: If a directed graph G consists of n vertices and m edges, then the incidence matrix is an n x m matrix C = [cij] and defined by 
The number of ones in an incidence matrix is equal to the number of edges in the graph. Example: Consider the directed graph G as shown in fig. Find its incidence matrix MI. 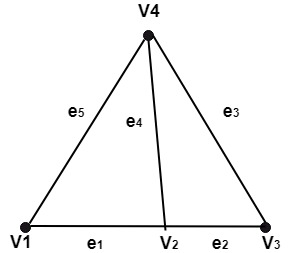
Solution: The directed graph consists of four vertices and five edges. Therefore, the incidence matrix is a 4 x 5 matrix which is show in fig: 
(c)Representation of Multigraph:Represented only by adjacency matrix representation. (i)Adjacency matrix representation of multigraph: If a multigraph G consists of vertices, then the adjacency matrix of graph is an n x n matrix A = [aij] and is defined by 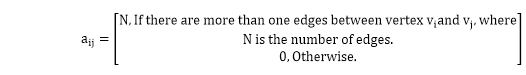
If there exist one or more than one edges between vertex vi and vj then aij=N, where is the number of edges between vi and vj. If there is no edge between vi and vj. Example: Consider the multigraph shown in Fig, Determine its adjacency matrix. 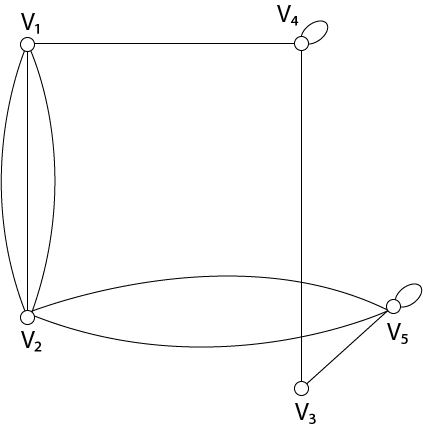
Solution: Since the multigraph consist of five vertices. Therefore the adjacency matrix will be an 5 x 5 matrix. The adjacency matrix of the multigraph is as follows: 
Next TopicIsomorphic and Homeomorphic Graphs
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









