Planer Graph in Discrete Mathematics

If we want to learn the planer graph, we have to know about the graph. The graph can be described as a collection of vertices, which are connected to each other with the help of a set of edges. We can also call the study of a graph as the Graph theory. In this section, we are able to learn about the definition of a planer graph, its properties, and examples of a Planer graph.

Planer Graph

A planer graph can be described as a graph that will be drawn in a plane in such a way that none of its edges cross each other. The simple example of a planer graph is described as follows: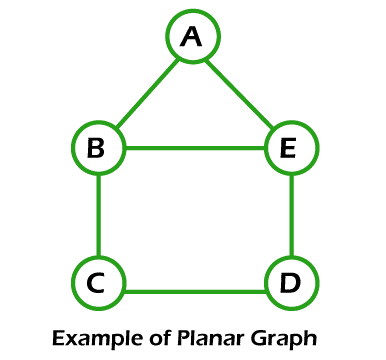

The above graph does not contain two edges that cross each other. Hence this graph is a planer graph.

Regions of plane:

In the process of planer representation of a graph, the plane is split into the connected areas, which are known as the regions of the plane.

There is some amount of degree which is associated with each region. These degrees are described as follows:

• Degree of Interior region is equal to the Number of edges enclosing that region.
• Same as, Degree of Exterior region is equal to the Number of edges exposed to that region.

Example of Region of plane:

In this example, we will consider a planer graph, which is described as follows: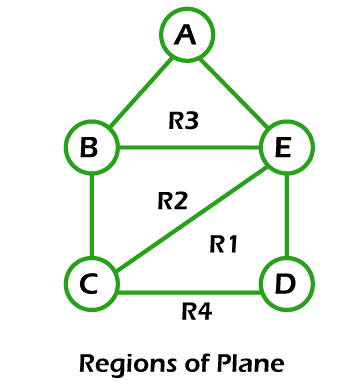

In the above planer graph, we can see that the graph splits the plane into 4 regions, i.e., R1, R2, R3, and R4, and the degree of these regions are described as follows:

Degree (R1) = 3
Degree (R2) = 3
Degree (R3) = 3
Degree (R4) = 5

Chromatic Number of Planer graph

• In any planer graph, the chromatic number must always be less than or equal to 4.
• Thus, to color the vertices of any planer graph, we always need a maximum of 4 colors.

Properties of Planer graph

There are various properties of a planer graph, and some of them are described as follows:

Property 1: The sum of degrees of all the vertices is equal to the total number of edges in the graph * 2. The symbolic representation of this property is described as follows: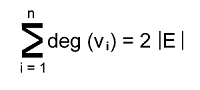

Property 2: The sum of degrees of all the regions is equal to the total number of edges in the graph * 2. The symbolic representation of this property is described as follows: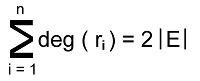

There are some special cases, which are described as follows:

Case 1: If the degree of each region is k, then the planer graph will contain the following relation:

Case 2: If the degree of each region is minimum k (>=k), then the planer graph will contain the following relation:

Case 3: If the degree of each region is maximum k (<=k), then the planer graph will contain the following relation:

Property 3: If there is a simple planer graph G, which contains the 'v' vertices, 'e' edges and 'r' number of regions, then the relation between them is described as follows:

We can call the above formula as Euler's formula.

In all the forms of planer representation of a graph, this formula remains the same.

Property 4: Suppose there is a planer graph G, which contains the k components. The relation between them is described as follows:

Examples of Planer graph:

There are various examples of planer graphs, and some of them are described as follows:

Example 1: In this example, we have a planer graph G, which contains 60 edges and 25 vertices. Now we have to determine the number of regions in graph G.

Solution: From the question, we have the following details about graph G:

Number of vertices (v) = 25

Number of edges (e) = 60

With the help of Euler's formula, we have r = e - v + 2.

Now we will put the values of v and e in this formula and get the following details:

r = 60 - 25 + 2

r = 37

Thus, the total number of region in graph G = 37.

Example 2: In this example, we have a simple planer graph G, which contains 9 edges and 10 vertices, and 3 components. Now we have to determine the number of regions in graph G.

Solution: From the question, we have the following details about graph G:

Number of vertices (v) = 10

Number of components (k) = 3

Number of edges (e) = 9

With the help of Euler's formula, we have r = e - v + (k+1).

Now we will put the values of v, e and k in this formula, and get the following details:

r = 9-10+ (3+1)

r = -1+4

r = 3

Thus, the total number of region in graph G = 3.

Example 3: In this example, we have a simple planer graph G, which contains 20 vertices and 3 as the degree of each vertex. Now we have to determine the number of regions in graph G.

Solution: From the question, we have the following details about graph G:

Degree of each vertex (d) = 3

Number of vertices (v) = 20

Calculating Total Number of Edges (e):

When we do the addition of a degree of vertices theorem, we have the following relation:

The Sum of degrees of all the vertices is equal to the Total number of edges * 2

Degree of each vertex * Number of vertices is equal to the Total number of edges * 2

So we will use the formula of degree of each vertex and get the following:

20*3 = 2*e

e = 30

Thus, in graph G, the total number of edges = 30.

Calculating Total number of Regions (r):

With the help of Euler's formula, we have r = e - v + 2.

When we put the values of v and e in this formula, we get the following details:

Number of regions (r) = 30-20+2

r = 12

Thus, in graph G, the total number of regions = 12.

Example 4: In this example, we have a simple planer graph G, which contains 35 regions and 6 as the degree of each region. Now we have to determine the number of vertices in graph G.

Solution: From the question, we have the following details about graph G:

Degree of each regions (d) = 6

Number of regions (n) = 35

Calculating Total Number of Edges (e):

When we do the addition of a degree of regions theorem, we have the following relation:

The Sum of degrees of all the regions is equal to the Total number of edges * 2

Degree of each region * Number of regions is equal to the Total number of edges * 2

35*6 = 2*e

e = 105

Thus, in graph G, the total number of edges = 105.

Calculating Total number of Vertices (v):

With the help of Euler's formula, we have r = e - v + 2.

When we will put the values of r and e in this formula, we get the following details:

35 = 105 - v + 2

v = 72

Thus, in graph G, the total number of vertices = 72.

Example 5: In this example, we have a simple planer graph G, which contains 30 edges, 12 vertices and k as the degree of each region. Now we have to determine the value of k.

Solution: From the question, we have the following details about graph G:

Number of edges (e) = 30

Degree of each regions (d) = k

Number of vertices (v) = 12

Calculating Total number of Regions (r):

With the help of Euler's formula, we have r = e - v + 2.

When we put the values of v, d, and e in this formula, we get the following details:

Number of regions (r) = 30-12+2

r = 20

Thus, in graph G, the total number of regions = 20.

Calculating the value of k:

When we do the addition of a degree of regions theorem, we have the following relation:

The Sum of degrees of all the regions is equal to the Total number of edges * 2

Degree of each region * Number of regions is equal to the Total number of edges * 2

20*k = 2*30

k = 30

Thus, in graph G, the Degree of each region = 3.

Example 6: In this example, we have a simple planer graph G, which contains 10 edges. Now we have to determine the maximum number of regions, which can be possible in this graph.

Solution: As we know that the simple planer graph contains the following things:

Degree of each region is >= 3.

So we have the following details:

3 * |R| <= 2 * |E|

Now we will put the value of |E| = 10, and get the following details:

3 * |R| <= 2* 10

|R| <= 6.67

|R| <= 6

Thus, in graph G, the maximum number of regions = 6.

Example 7: In this example, we have a simple planer graph G, which contains 15 regions. Now we have to determine the maximum number of edges, which can be possible in this graph.

Solution: As we know that the simple planer graph contains the following things:

Degree of each region is >= 3

So we have the following details:

3 * |R| <= 2 * |E|

Now we will put the value of |R| = 15, and get the following details:

3 * 15 <= 2* |E|

|E| >= 22.5

|E| >= 23

Thus, in graph G, the maximum number of edges = 23.