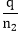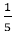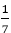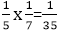Multiplication Theorem

Theorem: If A and B are two independent events, then the probability that both will occur is equal to the product of their individual probabilities.

          P(A∩B)=P(A)xP(B)

Proof: Let event
          A can happen is n₁ways of which p are successful
          B can happen is n₂ways of which q are successful
          Now, combine the successful event of A with successful event of B.
          Thus, the total number of successful cases = p x q
          We have, total number of cases = n₁ x n₂.
          Therefore, from definition of probability
          P (A and B) =P(A∩B)=
          We have P(A) =,P(B)=

          So,     P(A∩B)=P(A)xP(B)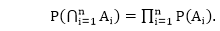
          If, there are three independent events A, B and C, then
          P(A∩B∩C)=P((A∩B)∩C)= P(A∩B)xP(C)
                            =P(A) x P(B) x P(C).
          In general, if there are n independent events, then

Example: A bag contains 5 green and 7 red balls. Two balls are drawn. Find the probability that one is green and the other is red.

Solution: P(A) =P(a green ball) =
                P(B) =P(a red ball) =
      By Multiplication Theorem
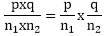
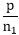      P(A) and P(B) = P(A) x P(B) =