Generating FunctionsGenerating function is a method to solve the recurrence relations. Let us consider, the sequence a0, a1, a2....ar of real numbers. For some interval of real numbers containing zero values at t is given, the function G(t) is defined by the series This function G(t) is called the generating function of the sequence ar. Now, for the constant sequence 1, 1, 1, 1.....the generating function is 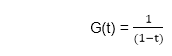
It can be expressed as G(t) =(1-t)-1=1+t+t2 +t3+t4+⋯[By binomial expansion] Comparing, this with equation (i), we get a0=1,a1=1,a2=1 and so on. For, the constant sequence 1,2,3,4,5,..the generating function is Comparing, this with equation (i), we get The generating function of Zr,(Z≠0 and Z is a constant)is given by Also,If a(1)r has the generating function G1(t) and a(2)r has the generating function G2(t), then λ1 a(1)r+λ2 a(2)r has the generating function λ1 G1(t)+ λ2 G2(t). Here λ1 and λ2 are constants. Application Areas:Generating functions can be used for the following purposes -
Example: Solve the recurrence relation ar+2-3ar+1+2ar=0 By the method of generating functions with the initial conditions a0=2 and a1=3. Solution: Let us assume that 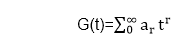
Multiply equation (i) by tr and summing from r = 0 to ∞, we have 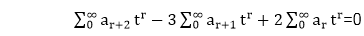
(a2+a3 t+a4 t2+⋯)-3(a1+a2 t+a3 t2+⋯)+2(a0+a1 t+a2 t2+⋯)=0
Now, put a0=2 and a1=3 in equation (ii) and solving, we get 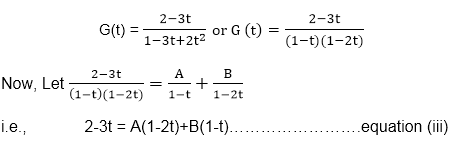
Put t=1 on both sides of equation (iii) to find A. Hence Put t= Thus G (t) =
Next TopicProbability
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





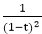 because it can be expressed as
because it can be expressed as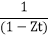 [Assume |Zt|<1]
[Assume |Zt|<1]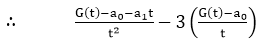 +2G(t)=0............equation (ii)
+2G(t)=0............equation (ii)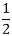 on both sides of equation (iii) to find B. Hence
on both sides of equation (iii) to find B. Hence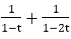 .Hence,ar=1+2r.
.Hence,ar=1+2r.




