Conjunction in Discrete Mathematics

Logical reasoning is an important skill that can be used in various fields like engineering, science, and as well as our daily life activities. We can also use logical reasoning in mathematical problem-solving strategies. With the help of logical reasoning and given facts, we can quickly get a conclusion. There are various kinds of logical connections to solve problems in mathematics. Some of them, the commonly used connectives are described as follows:

Implication
Negation
Disjunction
Equivalent
Conjunction

In this section, we are going to learn about one of the connectives called Conjunction. We will learn the definition, examples, rules, and truth tables of conjunction.

Definition of Conjunction

When we add the two statements with the help of 'AND' symbol, then it will be known as conjunction. For conjunctions, the combined compound statement will be true if and only if both statements are true.

Suppose there are two statements, i.e., "circles are curves" and "parallelograms are rectangle". Now we will make a compound statement by combining both statements with 'and' like this "circles are curves and parallelograms are rectangle". When both the statements are true, only then this newly created compound statement will be true. The compound statement will be false if only one statement is true and another one is false.

For example, the same would be true if the two statements were "Harry wants to become cricketer" and "Jack wants to become Engineer". If we combine both the statements with the help of 'and' to make "Harry wants to become cricketer and Jack wants to become engineer", then for this compound statement, both the statements must be true. The diagram of conjunction is described as follows:

Conjunction in Discrete mathematics

The conjunction can be described as a statement, which can be formed by adding two statements with the help of connector AND. The symbol ∧ is used for the conjunction. We can read this symbol as "and". If two statements, x, and y are joined in a statement, then the conjunction can be indicated symbolically in the form of x ∧ y. This statement will be true when both the combined statements are true. In all the other cases, it will be false. The conjunction of x and y is shown in the following image: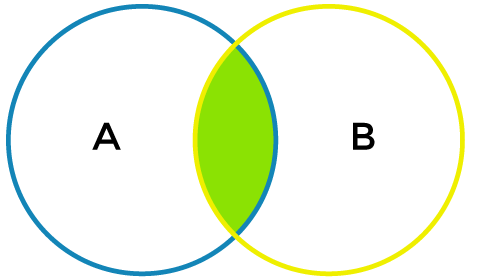

Rules of Conjunction

If both the combined statements are true, only then the conjunction statement will be true. In all the other cases, it will be false.
This process is very similar to AND gate, which is covered by the topic Gate logic.
The symbol ∧ is used to indicate the conjunction. We can read this symbol as "and", which is a type of logical connective.
We normally use the alphabetical letters to represent the statements. Suppose there are two statements, X and Y. When we add a conjunction connector, then the statement will become a compound statement. In this case, the compound statement is represented as X ∧ Y, and it will be read as "X and Y".

Conjunction Truth table

With the help of truth table, we can understand the final value of the compound statement, which is based on the values of individual statements. In the following truth table, all the possible combinations are represented. In the truth table, a true value is indicated with the help of letter 'T', and a false value is indicated with the help of letter 'F'. In the following truth table, we have two statements, X and Y, and a compound statement X ∧ Y. Now, we have to make a truth table of these statements.

X	Y	X ? Y
T	T	T
T	F	F
F	T	F
F	F	F

With the help of above table, we can see that when both the statements X and Y are true, only then the conjunction statement (X ∧ Y) is true. The conjunction statement is false when one of them is not true or false. In other words, we can say that the conjunction will be false in all the cases except when both the statements are true.

Examples of Conjunction

There are a lot of examples of conjunctions, which are described as follows:

Example 1: Suppose there are two statements, p, and q. Here, p: Harry is a cricket player and q: Jack is a tennis player. Now we have to determine whether it is a conjunction or not.

Solution: In this example, statement p indicates the sentence "Harry is a cricket player", and statement q indicates the sentence "Jack is a tennis player". The conjunction statement X ∧ Y will be true only when both the statements "Harry is a cricket player" and "Jack is a tennis player" are true statements. Otherwise, the conjunction will be false. Now, we will describe the truth table of all the possible combinations, which are described as follows:

X	Y	X ∧ Y
T	T	T
T	F	F
F	T	F
F	F	F

So we can see that when X and Y are true, only then the conjunction X ∧ Y is true. So the conjunction of both the statements is true.

Example 2: Suppose there are two statements, p, and q. Here, p: The number n is odd, and q: The number n is prime. Now, we have to determine whether the truth table can list all the truth values for X ∧ Y. If not, then determine why we cannot do that.

Solution: On the basis of variable n, the truth value of p ∧ q depends. But there are some infinite numbers also for n. Due to these values, the truth table cannot list all the truth values for p ∧ q. Without using the truth table, we can find the truth value of p ∧ q for the following values of n like this:

If n = 3, in this case, p is true, and q is true. So the conjunction p ∧ q is also true.

If n = 9, in this case, p is true, and q is false. So the conjunction p ∧ q is false.

If n = 2, in this case, p is false, and q is true. So the conjunction p ∧ q is false.

If n = 6, in this case, p is false, and q is false. So the conjunction p ∧ q is also false.

Example 3: In this example, we have to make a truth table for each conjunction, which is described as follows: