Total SolutionThe total solution or the general solution of a non-homogeneous linear difference equation with constant coefficients is the sum of the homogeneous solution and a particular solution. If no initial conditions are given, obtain n linear equations in n unknowns and solve them, if possible to get total solutions. If y(h) denotes the homogeneous solution of the recurrence relation and y(p) indicates the particular solution of the recurrence relation then, the total solution or the general solution y of the recurrence relation is given by Example: Solve the difference equation Solution: The homogeneous solution of this equation is obtained by putting R.H.S equal to zero i.e., The homogeneous solution is ar(h)= (C1+C2 r).2r The equation (i) can be written as (E2-4E+4) ar=3r+2r The particular solution is given as 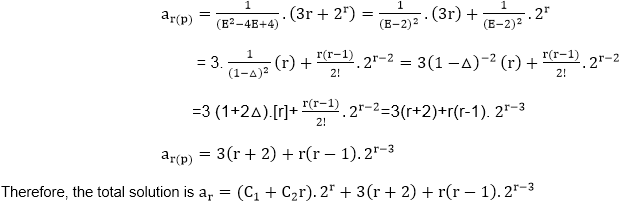
Next TopicGenerating Functions
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









