Lattices:Let L be a non-empty set closed under two binary operations called meet and join, denoted by ∧ and ∨. Then L is called a lattice if the following axioms hold where a, b, c are elements in L: 1) Commutative Law: - 2) Associative Law:- 3) Absorption Law: - Duality:The dual of any statement in a lattice (L,∧ ,∨ ) is defined to be a statement that is obtained by interchanging ∧ an ∨. For example, the dual of a ∧ (b ∨ a) = a ∨ a is a ∨ (b ∧ a )= a ∧ a Bounded Lattices:A lattice L is called a bounded lattice if it has greatest element 1 and a least element 0. Example:
Properties of Bounded Lattices:If L is a bounded lattice, then for any element a ∈ L, we have the following identities:
Theorem: Prove that every finite lattice L = {a1,a2,a3....an} is bounded. Proof: We have given the finite lattice: L = {a1,a2,a3....an} Thus, the greatest element of Lattices L is a1∨ a2∨ a3∨....∨an. Also, the least element of lattice L is a1∧ a2∧a3∧....∧an. Since, the greatest and least elements exist for every finite lattice. Hence, L is bounded. Sub-Lattices:Consider a non-empty subset L1 of a lattice L. Then L1 is called a sub-lattice of L if L1 itself is a lattice i.e., the operation of L i.e., a ∨ b ∈ L1 and a ∧ b ∈ L1 whenever a ∈ L1 and b ∈ L1. Example: Consider the lattice of all +ve integers I+ under the operation of divisibility. The lattice Dn of all divisors of n > 1 is a sub-lattice of I+. Determine all the sub-lattices of D30 that contain at least four elements, D30={1,2,3,5,6,10,15,30}. Solution: The sub-lattices of D30 that contain at least four elements are as follows: 1. {1, 2, 6, 30} 2. {1, 2, 3, 30} Isomorphic Lattices:Two lattices L1 and L2 are called isomorphic lattices if there is a bijection from L1 to L2 i.e., f: L1⟶ L2, such that f (a ∧ b) =f(a)∧ f(b) and f (a ∨ b) = f (a) ∨ f (b) Example: Determine whether the lattices shown in fig are isomorphic. Solution: The lattices shown in fig are isomorphic. Consider the mapping f = {(a, 1), (b, 2), (c, 3), (d, 4)}.For example f (b ∧ c) = f (a) = 1. Also, we have f (b) ∧ f(c) = 2 ∧ 3 = 1 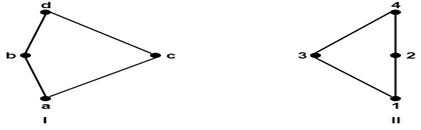
Distributive Lattice:A lattice L is called distributive lattice if for any elements a, b and c of L,it satisfies following distributive properties:
If the lattice L does not satisfies the above properties, it is called a non-distributive lattice. Example:
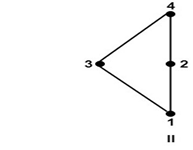
Complements and complemented lattices:Let L be a bounded lattice with lower bound o and upper bound I. Let a be an element if L. An element x in L is called a complement of a if a ∨ x = I and a ∧ x = 0 A lattice L is said to be complemented if L is bounded and every element in L has a complement. Example: Determine the complement of a and c in fig: 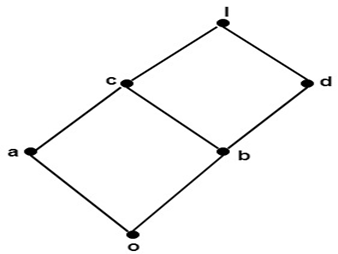
Solution: The complement of a is d. Since, a ∨ d = 1 and a ∧ d = 0 The complement of c does not exist. Since, there does not exist any element c such that c ∨ c'=1 and c ∧ c'= 0. Modular Lattice:A lattice (L, ∧,∨) is called a modular lattice if a ∨ (b ∧ c) = (a ∨ b) ∧ c whenever a ≤ c. Direct Product of Lattices:Let (L1 ∨1 ∧1)and (L2 ∨2 ∧2) be two lattices. Then (L, ∧,∨) is the direct product of lattices, where L = L1 x L2 in which the binary operation ∨(join) and ∧(meet) on L are such that for any (a1,b1)and (a2,b2) in L. (a1,b1)∨( a2,b2 )=(a1 ∨1 a2,b1 ∨2 b2) Example: Consider a lattice (L, ≤) as shown in fig. where L = {1, 2}. Determine the lattices (L2, ≤), where L2=L x L. 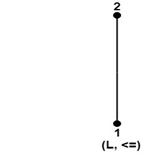
Solution: The lattice (L2, ≤) is shown in fig: 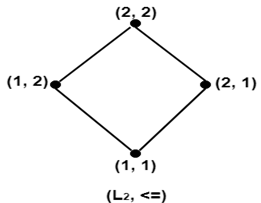
Next TopicBoolean Algebra
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









