Algebra of SetsSets under the operations of union, intersection, and complement satisfy various laws (identities) which are listed in Table 1. Table: Law of Algebra of Sets
Table 1 shows the law of algebra of sets. Example 1: Prove Idempotent Laws:Solution: Since, B ⊂ A ∪ B, therefore A ⊂ A ∪ A Let x ∈ A ∪ A ⇒ x ∈ A or x ∈ A ⇒ x ∈ A ∴ A ∪ A ⊂ A As A ∪ A ⊂ A and A ⊂ A ∪ A ⇒ A =A ∪ A. Hence Proved. Solution: Since, A ∩ B ⊂ B, therefore A ∩ A ⊂ A Let x ∈ A ⇒ x ∈ A and x ∈ A ⇒ x ∈ A ∩ A ∴ A ⊂ A ∩ A As A ∩ A ⊂ A and A ⊂ A ∩ A ⇒ A = A ∩ A. Hence Proved. Example 2: Prove Associative Laws:Solution: Let some x ∈ (A'∪ B) ∪ C ⇒ (x ∈ A or x ∈ B) or x ∈ C ⇒ x ∈ A or x ∈ B or x ∈ C ⇒ x ∈ A or (x ∈ B or x ∈ C) ⇒ x ∈ A or x ∈ B ∪ C ⇒ x ∈ A ∪ (B ∪ C). Similarly, if some x ∈ A ∪ (B ∪ C), then x ∈ (A ∪ B) ∪ C. Thus, any x ∈ A ∪ (B ∪ C) ⇔ x ∈ (A ∪ B) ∪ C. Hence Proved. Solution: Let some x ∈ A ∩ (B ∩ C) ⇒ x ∈ A and x ∈ B ∩ C ⇒ x ∈ A and (x ∈ B and x ∈ C) ⇒ x ∈ A and x ∈ B and x ∈ C ⇒ (x ∈ A and x ∈ B) and x ∈ C) ⇒ x ∈ A ∩ B and x ∈ C ⇒ x ∈ (A ∩ B) ∩ C. Similarly, if some x ∈ A ∩ (B ∩ C), then x ∈ (A ∩ B) ∩ C Thus, any x ∈ (A ∩ B) ∩ C ⇔ x ∈ A ∩ (B ∩ C). Hence Proved. Example3: Prove Commutative LawsSolution:
To Prove
A ∪ B = B ∪ A
A ∪ B = {x: x ∈ A or x ∈ B}
= {x: x ∈ B or x ∈ A} (∵ Order is not preserved in case of sets)
A ∪ B = B ∪ A. Hence Proved.
Solution:
To Prove
A ∩ B = B ∩ A
A ∩ B = {x: x ∈ A and x ∈ B}
= {x: x ∈ B and x ∈ A} (∵ Order is not preserved in case of sets)
A ∩ B = B ∩ A. Hence Proved.
Example 4: Prove Distributive LawsSolution:
To Prove
Let x ∈ A ∪ (B ∩ C) ⇒ x ∈ A or x ∈ B ∩ C
⇒ (x ∈ A or x ∈ A) or (x ∈ B and x ∈ C)
⇒ (x ∈ A or x ∈ B) and (x ∈ A or x ∈ C)
⇒ x ∈ A ∪ B and x ∈ A ∪ C
⇒ x ∈ (A ∪ B) ∩ (A ∪ C)
Therefore, A ∪ (B ∩ C) ⊂ (A ∪ B) ∩ (A ∪ C)............(i)
Again, Let y ∈ (A ∪ B) ∩ (A ∪ C) ⇒ y ∈ A ∪ B and y ∈ A ∪ C
⇒ (y ∈ A or y ∈ B) and (y ∈ A or y ∈ C)
⇒ (y ∈ A and y ∈ A) or (y ∈ B and y ∈ C)
⇒ y ∈ A or y ∈ B ∩ C
⇒ y ∈ A ∪ (B ∩ C)
Therefore, (A ∪ B) ∩ (A ∪ C) ⊂ A ∪ (B ∩ C)............(ii)
Combining (i) and (ii), we get A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C). Hence Proved
Solution:
To Prove
Let x ∈ A ∩ (B ∪ C) ⇒ x ∈ A and x ∈ B ∪ C
⇒ (x ∈ A and x ∈ A) and (x ∈ B or x ∈ C)
⇒ (x ∈ A and x ∈ B) or (x ∈ A and x ∈ C)
⇒ x ∈ A ∩ B or x ∈ A ∩ C
⇒ x ∈ (A ∩ B) ∪ (A ∪ C)
Therefore, A ∩ (B ∪ C) ⊂ (A ∩ B) ∪ (A ∪ C)............ (i)
Again, Let y ∈ (A ∩ B) ∪ (A ∪ C) ⇒ y ∈ A ∩ B or y ∈ A ∩ C
⇒ (y ∈ A and y ∈ B) or (y ∈ A and y ∈ C)
⇒ (y ∈ A or y ∈ A) and (y ∈ B or y ∈ C)
⇒ y ∈ A and y ∈ B ∪ C
⇒ y ∈ A ∩ (B ∪ C)
Therefore, (A ∩ B) ∪ (A ∪ C) ⊂ A ∩ (B ∪ C)............ (ii)
Combining (i) and (ii), we get A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∪ C). Hence Proved
Example 5: Prove De Morgan's Laws(a) (A ∪B)c=Ac∩ Bc Solution:
To Prove (A ∪B)c=Ac∩ Bc
Let x ∈ (A ∪B)c ⇒ x ∉ A ∪ B (∵ a ∈ A ⇔ a ∉ Ac)
⇒ x ∉ A and x ∉ B
⇒ x ∉ Ac and x ∉ Bc
⇒ x ∉ Ac∩ Bc
Therefore, (A ∪B)c ⊂ Ac∩ Bc............. (i)
Again, let x ∈ Ac∩ Bc ⇒ x ∈ Ac and x ∈ Bc
⇒ x ∉ A and x ∉ B
⇒ x ∉ A ∪ B
⇒ x ∈ (A ∪B)c
Therefore, Ac∩ Bc ⊂ (A ∪B)c............. (ii)
Combining (i) and (ii), we get Ac∩ Bc =(A ∪B)c. Hence Proved.
(b) (A ∩B)c = Ac∪ Bc Solution:
Let x ∈ (A ∩B)c ⇒ x ∉ A ∩ B (∵ a ∈ A ⇔ a ∉ Ac)
⇒ x ∉ A or x ∉ B
⇒ x ∈ Ac and x ∈ Bc
⇒ x ∈ Ac∪ Bc
∴ (A ∩B)c⊂ (A ∪B)c.................. (i)
Again, Let x ∈ Ac∪ Bc ⇒ x ∈ Ac or x ∈ Bc
⇒ x ∉ A or x ∉ B
⇒ x ∉ A ∩ B
⇒ x ∈ (A ∩B)c
∴ Ac∪ Bc⊂ (A ∩B)c.................... (ii)
Combining (i) and (ii), we get(A ∩B)c=Ac∪ Bc. Hence Proved.
Example 6: Prove Identity Laws.Solution:
To Prove A ∪ ∅ = A
Let x ∈ A ∪ ∅ ⇒ x ∈ A or x ∈ ∅
⇒ x ∈ A (∵x ∈ ∅, as ∅ is the null set )
Therefore, x ∈ A ∪ ∅ ⇒ x ∈ A
Hence, A ∪ ∅ ⊂ A.
We know that A ⊂ A ∪ B for any set B.
But for B = ∅, we have A ⊂ A ∪ ∅
From above, A ⊂ A ∪ ∅ , A ∪ ∅ ⊂ A ⇒ A = A ∪ ∅. Hence Proved.
Solution: To Prove A ∩ ∅ = ∅ If x ∈ A, then x ∉ ∅ (∵∅ is a null set) Therefore, x ∈ A, x ∉ ∅ ⇒ A ∩ ∅ = ∅. Hence Proved. Solution:
To Prove A ∪ U = U
Every set is a subset of a universal set.
∴ A ∪ U ⊆ U
Also, U ⊆ A ∪ U
Therefore, A ∪ U = U. Hence Proved.
Solution: To Prove A ∩ U = A We know A ∩ U ⊂ A................. (i) So we have to show that A ⊂ A ∩ U Let x ∈ A ⇒ x ∈ A and x ∈ U (∵ A ⊂ U so x ∈ A ⇒ x ∈ U ) ∴ x ∈ A ⇒ x ∈ A ∩ U ∴ A ⊂ A ∩ U................. (ii) From (i) and (ii), we get A ∩ U = A. Hence Proved. Example7: Prove Complement Laws(a) A ∪ Ac= U Solution:
To Prove A ∪ Ac= U
Every set is a subset of U
∴ A ∪ Ac ⊂ U.................. (i)
We have to show that U ⊆ A ∪ Ac
Let x ∈ U ⇒ x ∈ A or x ∉ A
⇒ x ∈ A or x ∈ Ac ⇒ x ∈ A ∪ Ac
∴ U ⊆ A ∪ Ac................... (ii)
From (i) and (ii), we get A ∪ Ac= U. Hence Proved.
(b) A ∩ Ac=∅ Solution:
As ∅ is the subset of every set
∴ ∅ ⊆ A ∩ Ac..................... (i)
We have to show that A ∩ Ac ⊆ ∅
Let x ∈ A ∩ Ac ⇒ x ∈ A and x ∈ Ac
⇒ x ∈ A and x ∉ A
⇒ x ∈ ∅
∴ A ∩ Ac ⊂∅..................... (ii)
From (i) and (ii), we get A∩ Ac=∅. Hence Proved.
(c) Uc= ∅ Solution:
Let x ∈ Uc ⇔ x ∉ U ⇔ x ∈ ∅
∴ Uc= ∅. Hence Proved. (As U is the Universal Set).
(d) ∅c = U Solution: Let x ∈ ∅c ⇔ x ∉ ∅ ⇔ x ∈ U (As ∅ is an empty set) ∴ ∅c = U. Hence Proved. Example8: Prove Involution Law(a) (Ac )c A. Solution:
Let x ∈ (Ac )c ⇔ x ∉ Ac⇔ x ∈ a
∴ (Ac )c =A. Hence Proved.
Duality:The dual E∗ of E is the equation obtained by replacing every occurrence of ∪, ∩, U and ∅ in E by ∩, ∪, ∅, and U, respectively. For example, the dual of It is noted as the principle of duality, that if any equation E is an identity, then its dual E∗ is also an identity. Principle of Extension:According to the Principle of Extension two sets, A and B are the same if and only if they have the same members. We denote equal sets by A=B. Cartesian product of two sets:The Cartesian Product of two sets P and Q in that order is the set of all ordered pairs whose first member belongs to the set P and second member belong to set Q and is denoted by P x Q, i.e., Example: Let P = {a, b, c} and Q = {k, l, m, n}. Determine the Cartesian product of P and Q. Solution: The Cartesian product of P and Q is 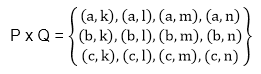
Next TopicMultisets
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










