Column matrix in discrete mathematicsA matrix will be known as a column matrix if it contains only one column. With the help of order m∗1, we can indicate the order of column matrix. Here m is used to indicate the number of rows, and 1 is the number of column. According to this order m∗1, the rows will contain only a single element, which is arranged in such a manner that they will indicate a column of elements. In any matrix, the rows and columns are used to contain the elements. We can indicate the row elements with the help of horizontal arrangement. We can indicate the column elements with the help of vertical arrangement. Suppose there is a matrix A = [aij], which contains an order m∗1. The column matrix will be indicated as follows: In this section, we will learn about what are column matrices, the properties of column matrices, operations on column matrices, and examples of column matrices. What is Column matrixA column matrix is a type of matrix in which all the elements are arranged in a single column. That means in a column matrix, there can be more than one row but only a single column. Suppose there is a matrix m∗n where m is used to indicate the number of rows and n is used to indicate the number of columns. In this order, if n = 1, then this type of matrix will be known as the column matrix. Thus, we can form a column matrix with the help of a vertical line of elements. A column matrix can be described as a rectangular array of elements that are arranged in the form of a vertical line. In the following way, we can indicate the general representation of the column matrix. 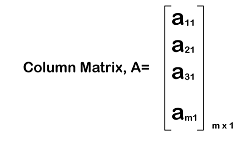
If the order of a matrix is 1∗1, only then we can find the determinant of a column matrix. We cannot define the determinant of a column matrix if there is an order m∗1 where the value of m is greater than 1. Therefore, we can define the determinants only for the square matrix. Now we will show some examples so that we can better understand the concept of column matrix. Properties of Column matrixWe can deeply understand the concept of a column matrix with the help of some properties, which are described as follows:
Operations on Column matrixIn the field of discrete mathematics, there are various kinds of operations that can be performed on column matrices, i.e., multiplication, subtraction, addition, and division. While performing the addition and subtraction operation, we can take any other matrix to do that. If there is a column matrix, then we can perform addition or subtraction operations to any other column matrix only. For the addition or subtraction operation on column matrices, the order of these matrices must be the same. 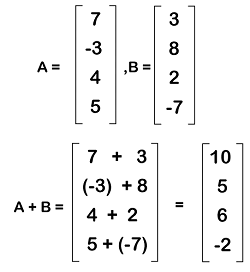
With the help of a row matrix, we will be able to do the multiplication of a column matrix. For matrix multiplication, we have to satisfy its condition, i.e., the number of columns in the 1st matrix and the number of rows in the 2nd matrix must be similar to each other. That means in case of multiplication operation, the number of columns in the column matrix and the number of rows in the matrix are similar to each other. 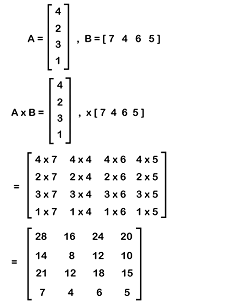
When we do the multiplication of column matrix with the help of a row matrix, then the generated result will be a square matrix. If we want to do the inverse of column matrix, then it will not be possible, and because of this reason, we cannot use the column matrix for division operation. That means the column matrix can be performed on addition, subtraction, and multiplication but not on division. Examples of column matrix on the basis of orderHere we will show the column matrices with different orders, which are described as follows: Example 1: In this example, we will show a column matrix with an order 1∗1, i.e., A = [5] In this matrix, we can see that there is only 1 element, which is arranged in the form of 1 row and 1 column. In the matrix A = [5], the determinant is 5. Example 2: In this example, we will show a column matrix with an order 2∗1, which is described as follows: 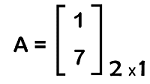
In this matrix, we can see that there are 2 elements, which are arranged in the form of 2 rows and 1 column. Example 3: In this example, we will show a column matrix with an order 3∗1, which is described as follows: 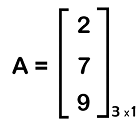
In this matrix, we can see that there are 3 elements, which are arranged in the form of 3 rows and 1 column. Example 4: In this example, we will show a column matrix with an order 4∗1, which is described as follows: 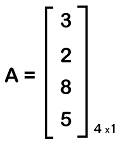
In this matrix, we can see that there are 4 elements, which are arranged in the form of 4 rows and 1 column. Example 5: In this example, we will show a column matrix with an order 5∗1, which is described as follows: 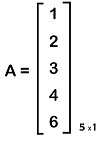
In this matrix, we can see that there are 5 elements, which are arranged in the form of 5 rows and 1 column. Example 6: In this example, we will show a column matrix with an order 6∗1, which is described as follows: 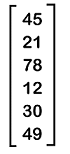
In this matrix, we can see that there are 6 elements, which are arranged in the form of 6 rows and 1 column. All the above examples are known as column matrices because all the elements of these matrices are arranged in a single column. Examples of Column matrixThere are a lot of examples of column matrices, and some of them are described as follows: Example 1: In this example, we have a column matrix, and we have to perform transpose of that matrix. The column matrix is described as follows: 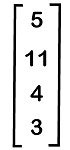
Solution: From the question, we have a column matrix A where 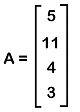
We can perform the transpose of the column matrix by writing all the elements of the column matrix in the form of row elements. AT = [5 11 4 3] Hence, row matrix is the transpose of the column matrix. Example 2: In this example, we have a row matrix [2 6 9] and a column matrix, and we have to do the multiplication of both matrices. The column matrix is described as follows: 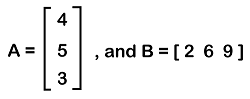
Solution: From the question, we have a column matrix and row matrix like this: 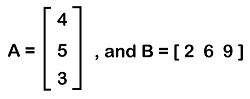
The multiplication of column matrix and row matrix is described as follows: 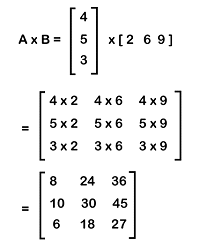
Therefore, the multiplication of row matrix and the column matrix is a singleton matrix.
Next TopicZero matrix in Discrete mathematics
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









