Normal SubGroup:Let G be a group. A subgroup H of G is said to be a normal subgroup of G if for all h∈ H and x∈ G, x h x-1∈ H If x H x-1 = {x h x-1| h ∈ H} then H is normal in G if and only if xH x-1⊆H, ∀ x∈ G Statement: If G is an abelian group, then every subgroup H of G is normal in G. Proof: Let any h∈ H, x∈ G, then Hence H is normal subgroup of G. Group Homomorphism:A homomorphism is a mapping f: G→ G' such that f (xy) =f(x) f(y), ∀ x, y ∈ G. The mapping f preserves the group operation although the binary operations of the group G and G' are different. Above condition is called the homomorphism condition. Kernel of Homomorphism: - The Kernel of a homomorphism f from a group G to a group G' with identity e' is the set {x∈ G | f(x) =e'} The kernel of f is denoted by Ker f. If f: G→G' is a homomorphism of G intoG', then the image set of f is the range, denoted by f (G), of the map f. Thus Im (f) = f (G) = {f(x)∈ G'| x ∈G} If f (G) =G', then G' is called a homomorphic image of G. Note: - A group homomorphismIsomorphism:Let (G1,*) and (G2,0) be two algebraic system, where * and 0 both are binary operations. The systems (G1,*) and (G2,0) are said to be isomorphic if there exists an isomorphic mapping f: G1→G2 When two algebraic systems are isomorphic, the systems are structurally equivalent and one can be obtained from another by simply remaining the elements and operation. Example: Let (A1,*) and (A2,⊡) be the two algebraic systems as shown in fig. Determine whether the two algebraic systems are isomorphic. 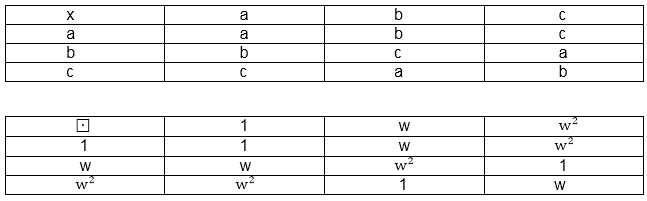
Solution: The two algebraic system (A1,*) and (A2,⊡) are isomorphic and (A2,⊡) is an isomorphic image of A1, such that f( a)=1 Automorphism:Let (G1,*) and (G2,0) be two algebraic system, where * and 0 both are binary operations on G1 and G2 respectively. Then an isomorphism from (G1,*) to (G2,0) is called an automorphism if G1= G2 Rings:An algebraic system (R, +,) where R is a set with two arbitrary binary operations + and ., is called aring if it satisfies the following conditions
Example1: Consider M be the set of all matrices of the type Example2: The set Z9 = {0, 1, 2, 3, 4, 5, 6, 7, 8} under the operation addition and multiplication modulo 9 forms a ring. Types of Rings:1. Commutative Rings: A ring (R, +,) is called a commutative ring if it holds the commutative law under the operation of multiplication i.e., a. b = b. a, for every a, b∈ R Example1: Consider a set E of all even integers under the operation of addition and multiplication. The set E forms a commutative ring. 2. Ring with Unity: A ring (R, +,) is called a ring with unity, if it has a multiplicative identity i.e, Example: Consider a set M of all 2 x 2 matrices over integers under matrix multiplication and matrix addition. The set M forms a ring with unity 3. Ring with Zero Divisions: If a.b=0, where a and b are any two non-zero elements of R in the ring (R, +) then a and b are called divisions of zero and the ring (R, +) is called ring with zero division. 4. Rings without Zero Division: An algebraic system (R, +) where R is a set with two arbitrary binary operation + and is called a ring without divisors of zero if for every a, b ∈R, we have a.b≠0 ⟹a≠0 and b ≠0 SubRings:A subset A of a ring (R, +) is called a subring of R, if it satisfies following conditions: (A, +) is a subgroup of the group (R,+) A is closed under the multiplication operation i.e., a.b ∈A,for every a,b ∈A. Example: The ring (I, +) of integers is a subring of ring (R, +) of real numbers. Note:
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





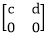 over integers under matrix addition and matrix multiplication. Thus M form a ring.
over integers under matrix addition and matrix multiplication. Thus M form a ring.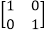 .
.




