Multinomial TheoremThe multinomial theorem is used to expand the power of a sum of two terms or more than two terms. The multinomial theorem is mainly used to generalize the binomial theorem to polynomials with terms that can have any number. The weighted sum of monomials can express a power (x1 + x2 + x3+ ….. + xk)n in the form x1b1, x2b2, x3b3 ….. xkbk. Where, the generalizations of binomial coefficients, which can be known as multinomial coefficients, are used to provide the weights. The corresponding multinomial series can appear with the help of multinomial distribution, which can be described as a generalization of the binomial distribution. With the help of this theorem, we can describe the result of expanding the power of multinomial. In order to expand an expression, the multinomial theorem provides a formula, which is described as follows: (x1 + x2 +⋯+ xk)n for integer values of n We can expand this formula in the following way: 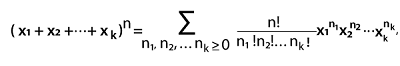
Where n = n1 + n2 + n3 + …. + nk and n! is used to describe the factorial notation for 1*2*3* …. *n. CoefficientIn algebra, we have to first learn about how we can read algebraic equations. A number of terms are contained in the algebraic structure, which is added or subtracted together. In algebra, each and every term consists of two parts that are variables and coefficients. In statistics, there is a different type of coefficient, which is known as the multinomial coefficient. Now we will learn about the uses of multinomial coefficients in statistics. Multinomial CoefficientThe multinomial coefficient uses the multinomial series and then gets its name. This series is raised to the nth power, which is described as follows: (x1 + x2 + x3 + ….. + xk)n In the above series, x is used to describe the terms. The k is used to describe the number of elements that exist in the series. The n is used to describe the positive integer power to which series is raised. The multinomial theorem describes that how this type of series is expanded, which is described as follows: 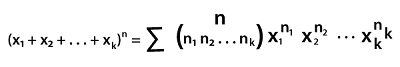
The sum is taken over n1, n2, n3, … , nk in the multinomial theorem like n1 + n2 + n3 + ….. + nk = n. The multinomial coefficient is used to provide the sum of multinomial coefficient, which is multiplied using the variables. It is used to represent the expanded series, and each term in this series contains its associated multinomial coefficient. In terms of factorials, the multinomial coefficient will be expressed itself, which is described as follows: 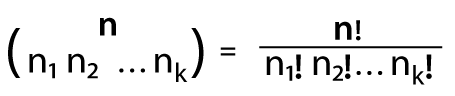
Examples of Multinomial theoremExample 1: In this example, we will expand (x + y + z)3 like the following way
(x + y + z)3 = (x + y + z) (x + y + z) (x + y + z)
= x3 + y3 + z3
+ 3x2y + 3x2z + 3xy2 + 3xz2 + 3y2z + 3yz2
+ 6xyz
Example 2: In this example, we will describe that how multinomial theorem works for a trinomial. For this, we will assume (x + y + z)4. If we use brute force to expand this expression, then it will be written as follows:
(x + y + z) (x + y + z) (x + y + z) (x + y + z)
Now we will apply the distribution law. After that, we will simplify by collecting like terms. This expression has 81 terms before collecting and after distributing. The reason behind 81 terms is that every term in the first bracket will be multiplied by every term in the second bracket, which will provide us 9 terms. Now every given term means 9 terms will be multiplied with every term in the third bracket, which will provide us 27 terms. Lastly, every giving term that means 27 terms will be multiplied with every term in the fourth bracket, which will provide us 81 terms. Before simplifying, a lot of terms will look different, but when we simplify it, then it will look identical. For example: Suppose we have four terms xyyy, yxyy, yyxy, and yyyx. In these terms, x comes from either the first, second, third, or fourth brackets. When we simplify these terms, then they will be collected and provide as 4xy3.
(x + y + z)4 = (x + y + z) (x + y + z) (x + y + z) (x + y + z)
= x4 + y4 + z4
+ 4xy3 + 4xz3 + 4x3y + 4x3z + 4yz3 + 4y3z
+ 12 xyz2 + 12 xy2z + 12 x2yz
+ 6x2y2 + 6x2z2 + 6y2z2
In this above expansion, we can see that we have total 15 distinct terms, and each term contains degree 4. The coefficient adds up to 34 = 81. Now we will use the steps to construct this expansion and derive the multinomial theorem like this: Step 1: We will use the three nested summations to start this: 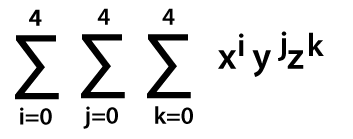
The problem we face while doing this is that the triple summation generates 5*5*5 = 125 terms of various degrees, describing the range from x0y0z0 to x4y4z4. Step 2: Now, we will add a filter factor, which is equal to 0 for unwanted terms and 1 for wanted terms. This is known as the Kronecker delta function, and it is denoted by δi, j. The syntax to define this is as follows: 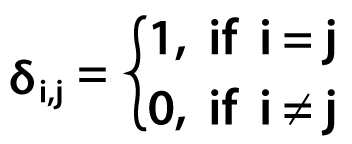
Now we will change this summation for reading like this: 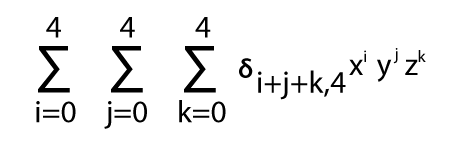
The above summation contains the 15 wanted terms only, which has degree 4. Now we have a single problem that is every coefficient equals to 1. Step 3: Now, we will construct the correct coefficient. This coefficient will be known as the multinomial coefficient like this: 
The number of ways to deposit 4 distinct objects into 3 distinct groups will be provided by the above multinomial coefficient. Objects i will be deposit into the first group. Objects j will be deposit into the second group, and objects k will be deposit into the third group. It does not matter that in which order we are depositing them. For example: In the coefficient of term x1y1z2 uses i = 1, j = 1, and k = 2, which will be equal to 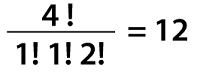
With the above coefficient, the expansion will be read as follows: 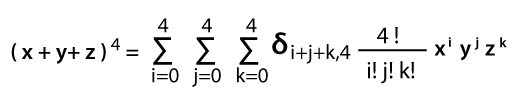
For nth power The above four terms can be generalized into the nth power of a trinomial. For this, we have to change all 4's to n's. 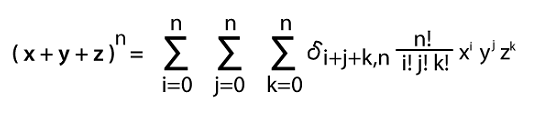
This is known as the multinomial theorem for 3 terms. We can easily generalize the nth term into any number of terms. For example: for 4 terms, the multinomial theorem will be read as follows: 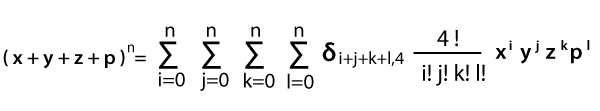
Next TopicLagrange's Mean Value Theorem
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










