Types of Functions1. Injective (One-to-One) Functions: A function in which one element of Domain Set is connected to one element of Co-Domain Set. 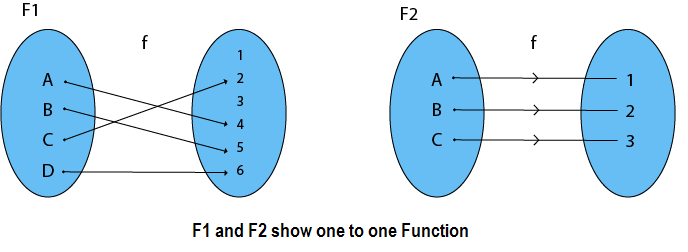
2. Surjective (Onto) Functions: A function in which every element of Co-Domain Set has one pre-image. Example: Consider, A = {1, 2, 3, 4}, B = {a, b, c} and f = {(1, b), (2, a), (3, c), (4, c)}. It is a Surjective Function, as every element of B is the image of some A 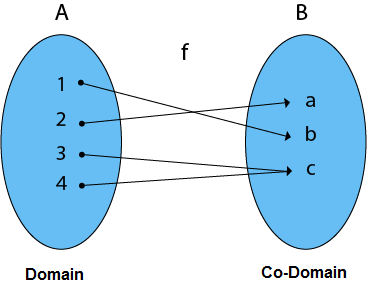
Note: In an Onto Function, Range is equal to Co-Domain.3. Bijective (One-to-One Onto) Functions: A function which is both injective (one to - one) and surjective (onto) is called bijective (One-to-One Onto) Function. 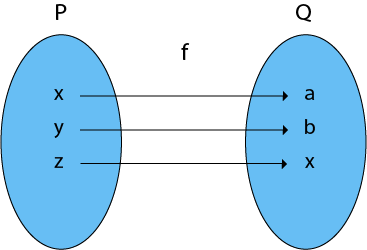
Example: The f is a one-to-one function and also it is onto. So it is a bijective function. 4. Into Functions: A function in which there must be an element of co-domain Y does not have a pre-image in domain X. Example: Therefore, it is an into function 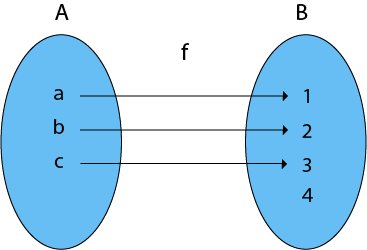 5. One-One Into Functions: Let f: X → Y. The function f is called one-one into function if different elements of X have different unique images of Y. Example: The function f is a one-one into function 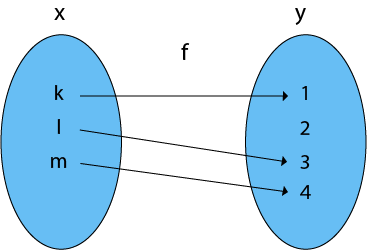 6. Many-One Functions: Let f: X → Y. The function f is said to be many-one functions if there exist two or more than two different elements in X having the same image in Y. Example: The function f is a many-one function 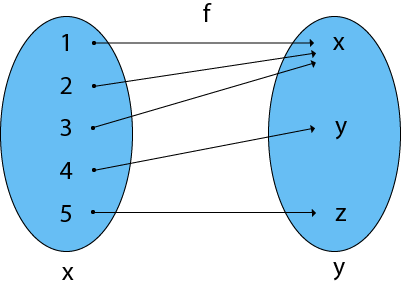 7. Many-One Into Functions: Let f: X → Y. The function f is called the many-one function if and only if is both many one and into function. Example: As the function f is a many-one and into, so it is a many-one into function. 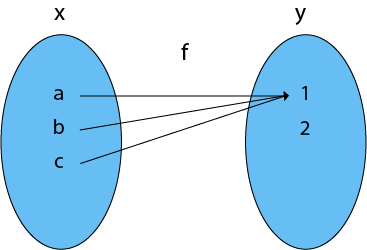 8. Many-One Onto Functions: Let f: X → Y. The function f is called many-one onto function if and only if is both many one and onto. Example: The function f is a many-one (as the two elements have the same image in Y) and it is onto (as every element of Y is the image of some element X). So, it is many-one onto function 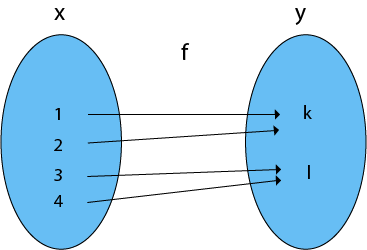
Next TopicIdentity Functions
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










