Identity Function in Discrete mathematics

The identity function is a special type of linear function which is used to return the same output as input. That means in the identity function, the output and inputs are the same. We can also call an identity function as an identity relation or identity map. For an identity function, the range value and domain value are equal to each other.

In other words, we can say that if a function returns the same values as output that we used as an input, then this type of function will be known as the identity function. In this section, we are going to learn about the definition of identity functions, their properties, and examples.

Definition of Identity function in Math

A function will be known as the identity function if each element in set B gives images of itself, i.e., g(b) = b ∀ b ∈ B. The identity function is indicated by the symbol "I". Suppose there is a function g. The identity function for an argument x will be indicated as g(x) = x. In the domain, the image of an element is similar to the output in the range. That's why we call this function an identity function. Each and every real number is mapped with itself in an identity function. In this function, the input and output are similar to each other. We can very easily find whether the given function is an identity function or not because in the identity function, the image and pre-image are identical.

To explain this, we will consider an example of a function where we have to map the elements of set A to itself. Here A = {1, 2, 3, 4, 5}, and g: A → A. We have to map g like this g = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5)}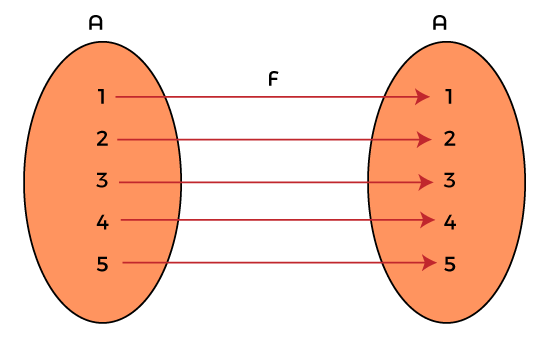

In the above image, each element of set A is mapped onto itself. So the function f is an identity function. This is why the function f is also onto and one to one function.

Domain, Range, and Inverse of Identity function

An identity function can be described as a real-valued function, which is indicated as g: R → R in a way that g(x) = x for each x ∈ R. Here R is used to indicate a set of real numbers, which is the domain of function g. For the identity function, the range and domain are the same. That means if we enter input as 90, then the result/output will also be 90. If our input is 0, then the result/output of an identify function will also be 0. Some important points related to the domain, range, and inverse in an identity function are described as follows:

• R will be the domain of an identity function g(x).
• R will also be the range of an identity function.
• In the identity function, the range and co-domain are equal sets. That means this function is onto.
• If we do inverse of any function, in this case, the range and domain of that function are swapped. Due to this, we can say that the identity function is invertible, and this function is also its own inverse.

Graph of an Identity function

When we want to plot a graph of an identity function, then we need to use the x-axis and y-axis. The x-axis will be used to plot the values of x coordinates, and the y-axis will be used to plot the values of y coordinates. The graph of an identity function will always be a straight line that passes by the origin. In this function, the range and domain are equal to each other.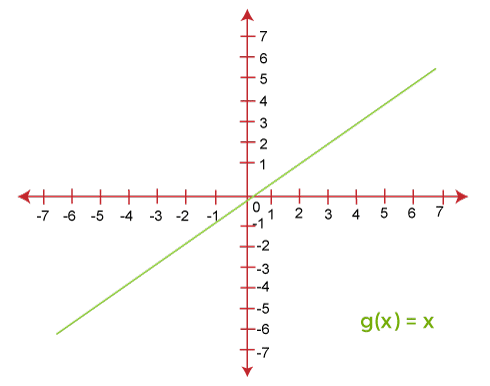

In the above graph, we get a straight line, which makes a 45° angle on both the axis (x-axis and y-axis). In the graph of an identity function, the slope will always remain 1.

Properties of Identity function:

In a function, if we want the return the exact value of the argument, in this case, the identity function is used. We should not be confused between the null function, empty function, or identity function because there is a big difference between them. In the identity function, some important properties are described as follows:

• If there is a case of application of vector spaces, then the identity function will be a linear operator.
• It will be a multiplicative function if there are positive integers.
• The identity function is a type of real-valued linear function.
• The graph of this function is equal to its inverse.
• The identity function will be expressed as identity matrix I_m if there is m dimensional vector space.
• This function will always be continuous in the case of topological space.

Important Notes:

When we study the identity function, we have to keep in mind some points, which are described as follows:

• For the identity function, the range and domain are similar to each other.
• In the identity function graph, the slop always remains as 1.

Example of Identity function

There are a lot of examples identity functions. Some of them are described as follows:

Example 1: In this example, we have to prove that g ◦ g is an identity function if g(y) = (2y + 3) / (3y - 2).

Solution: Here g(y) = (2y + 3) / (3y - 2)

g ◦ g(y) = g(g(y)) = g((2y + 3) / (3y - 2))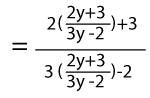

= (4y + 6 + 9y - 6) / (6y + 9 - 6y + 4)

= 13y / 13

= y

Hence g ◦ g(y) = y. So we can say that g ◦ g(y) is an identity function.

Example 2: In this example, we have to prove that f(2x) = 2x is an identity function.

Solution: Here, f(2x) = 2x

Now we will put the values of x in the above function like this:

If x = 1, then the function will be

f(2(1)) = 2(1)

f(2) = 2

If x = 2, then the function will be

f(2(2)) = 2(2)

f(4) = 4

If x = 3, then the function will be

f(2(3)) = 2(3)

f(6) = 6

Now we will try some negative values of x and put it into the function like this:

If x = -1, then the function will be

f(2(-1)) = 2(-1)

f(-2) = -2

If x = -2, then the function will be

f(2(-2)) = 2(-2)

f(-4) = -4

If x = -3, then the function will be

f(2(-3)) = 2(-3)

f(-6) = -6

Now we will show a table for all the above values of x

x	-3	-2	-1	0	1	2	3
y = f(x)	-6	-4	-2	0	2	4	6

Now we will draw a graph for all these values like this: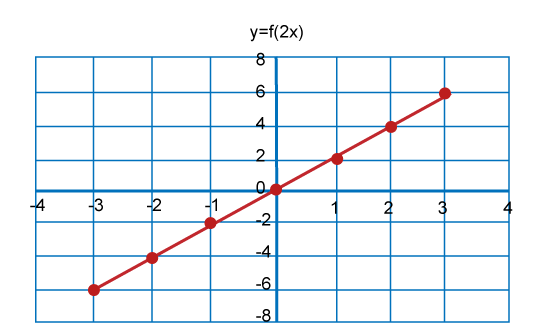

In the above graph, we can see that a straight line plot by the function f(2x) = 2x. Hence, this function is an identity function.

Example 3: In this example, we will consider a range of identity functions in which the number of elements of a set has total 9 elements. Now we have to choose that range from the following options:

1. 3²
2. 3⁴
3. 3⁸
4. 3¹⁶

Solution: The first option (3²) is the correct option in all the options. As we know that if the given element is related to itself, then it will be known as the identity function, i.e., g(x) = x. So if there are 9 elements in a set, then the range of that function will also be 9, and here 3² = 9. Hence, range 3² contains total 9 elements.

---

Next TopicInjective Function in Discrete mathematics

← prev next →