Continuous Functions in Discrete mathematicsA continuous function can be described as a function whose graph will always be continuous without any jump or break. That means a given function will be continuous if we will successfully draw the graph (curve) of a function without even lifting the pencil. In discrete mathematics, it is very important to learn about the continuous function. Now we will learn more about the continuous function by learning the definition and examples of continuous functions. Definition of Continuous functionSuppose we have a function f(x). If the curve of the given function f(x) will not break at the given point x = a, only then this function will be known as continuous at point x = a. There is also a mathematical definition of continuous function, which is described as follows: A given function f(x) will be continuous at point 'x = a' if it satisfies the following conditions:
Now we will check that the above mathematical definition actually provides the meaning that the function does not break at x = a? We will do this to check the above points. The limx → a f(x) exist is used to indicate that the function should approach the same value x = a from both the sides, left side and right side. The 'limx → a f(x) = f(a)' is used to indicate that the limit of function at x = a is equal to the f(a). So we can say that when we put these two conditions together, after that, the given function becomes continuous at x = a without any break. With the help of below image, we can understand this concept more. 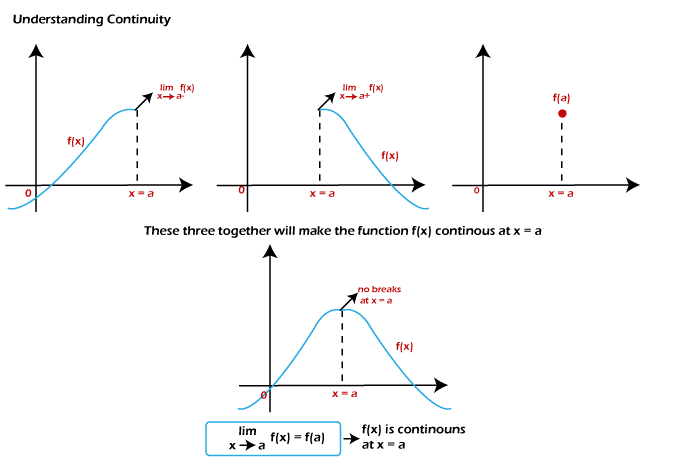
A function will be known as continuous over an interval if and only if this function is continuous at each point on the interval. That means for a continuous function, the graph of this function should not jump or break over that interval. Examples of Continuous functionThere are a lot of examples of continuous functions. In the below images, all the functions are continuous over respective domains. 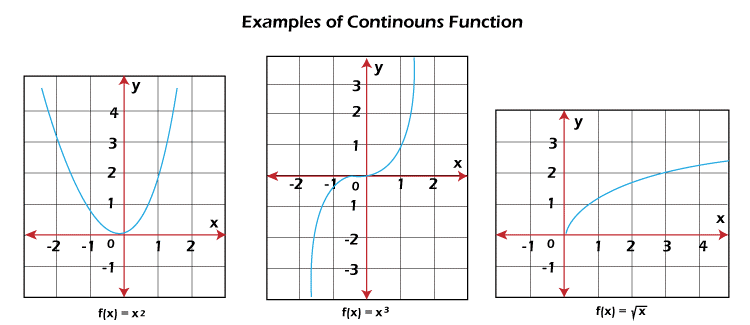
Properties of a Continuous functionThere are various properties of continuous functions. If there are two continuous functions f(x) and g(x), at x = a, then the following properties will be held by these functions:
Theorems on Continuous functionWe have a lot of theorems on the continuous functions. Some of the important theorems are described as follows: Theorem 1: On (-∞, ∞), all the polynomial functions will be continuous. Theorem 2: On (-∞, ∞), the functions cos x, sin x, ex, and arctan x will be continuous. Theorem 3: Suppose there are two functions, f and g, which are continuous over the interval [a, b], then fg, f+g, and f-g will be continuous on [a, b]. But f/g is continuous on [a, b] given that f/g is NOT zero anywhere in the interval. Theorem 4: All the rational functions will be continuous except the vertical asymptotes. Theorem 4: All the rational functions will be continuous except the vertical asymptotes. Not Continuous function in a discrete mathematicsIf there is a function that is not continuous, then it will be known as the discontinuous function. That means the graph of a discontinuous function must jump or break somewhere. We have various types of discontinuity functions like JUMP Discontinuity, Removable discontinuity, and Infinite discontinuity. So the function will not be continuous or discontinuous in any one of these cases. In the following image, we will see all types of discontinuities. With the help of the following image, we can understand some things, which are described as follows:
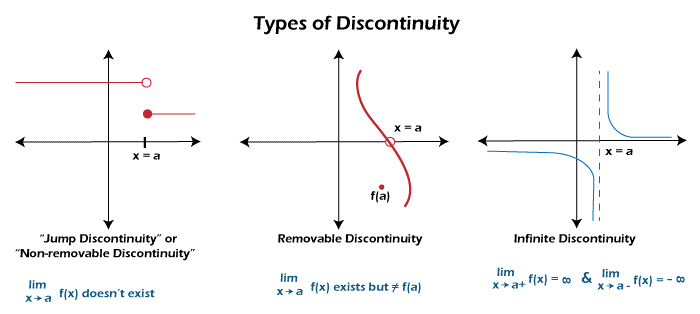
Jump Discontinuity The jump discontinuity is also known as the non-removable discontinuity. In the jump discontinuity, limₓ → ₐ? f(x) and limₓ → ₐ? f(x) exists, but they are not equal. Removable Discontinuity In the removable discontinuity, the limₓ → ₐ f(x) exist, i.e., limₓ → ₐ? f(x) = limₓ → ₐ? f(x)), but this limit is Not same as f(a). Infinite Discontinuity If there are two limits limₓ → ₐ? f(x) and limₓ → ₐ? f(x), then the values of one or both the limits will be ± ∞. Important Notes on Continuous function:In the continuous function, there are some points which we should keep in our mind while learning this, which are described as follows:
Examples of Continuous functionsThere are various examples of continuous functions, which are described as follows: There are various examples of continuous functions, which are described as follows: Example 1: In this example, we have to check whether the given function is continuous at a point x = 7. Here function f(x) = 5x-8. Solution: We can do this with the help of two methods. Method 1: From the above question, we have f(x) = 5x-8 and x = 5 = a. Here we will determine limₓ → ₐ f(x) and f(a). limₓ → ₐ f(x) = limₓ → 5 (5x - 8) = 5(5) - 8 = 25-8 = 17. f(a) = f(5) = 5(5) - 8 = 25-8 = 17 Therefore, limₓ → ₐ f(x) = f(a). Hence, we can say that the given function f(x) = 5x-8 is continuous at x = 5. Method 2: As we have learned that a polynomial function is continuous everywhere. Here polynomial function is shown by the given function f(x) = 5x-8. The function will be continuous everywhere. Hence it will be continuous at the given point x = 5. In conclusion, we can say that the function f(x) = 5x-8 is continuous at point x=5. Example 2: In this example, we have to show that the function f(x) is Not continuous at the point x = 2. We have to prove the same thing with the help of its graph. We have to also show the type of discontinuity. The function f(x) is described as follows: 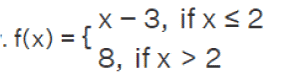
Solution: From the question, we have a = 2. x→ 5- ⇒ x < 5 ⇒ f(x) = x-7 and x→ 5+ ⇒ x > 5 ⇒ f(x) = 6. Now we will compute the limits like this: limₓ → 5- f(x) = limₓ → 5 (x-7) = 5-7 = -2 limₓ → 5+ f(x) = limₓ → 5 6 = 6 Here, limₓ → 5- f(x) ≠ limₓ → 5+ f(x). Thus, limₓ → 5 f(x) does not exist, and hence we can say that f(x) is not continuous at point x = 2. Now we will verify it with the help of following graph: 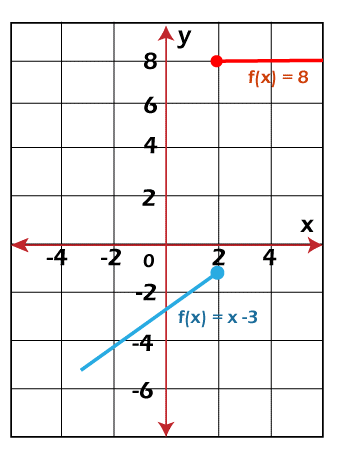
From the above graph, we can say that the function has a jump discontinuity. In conclusion, we have proved that graphically and algebraically, f(x) is discontinuous, and this function has a jump discontinuity. Example 3: In this example, we have to determine the relation between a and b if the given function is continuous at x = 4. Here function f(x) is described as follows: 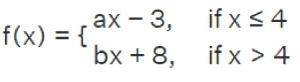
Solution: The given function f(x) is continuous at point x = 4. With the help of continuous function, we will get the following equation: limₓ → 5- f(x) = limₓ → 5+ f(x) = f(5) limₓ → 5 (ax-7) = limₓ → 5 (bx+6) = a(5) - 7 a(5) - 7 = b(5)+6 = a(5) - 7 With the help of first two equations, we will get the following: 5a-7 = 5b+6 5a-5b = 13 Hence, we can say that the relation between a and b is 5a-5b = 13.
Next Topic#
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









