Hypergeometric Distribution in Discrete MathematicsHypergeometric distribution can be described as the probability distribution of a hypergeometric random variable. In the hypergeometric distribution, we will consider an attribute and a population. Here attributes are used to take one of two states, and these states must be mutually exclusive. One of these two states contains every member of the population. For example: "under or over 25 years old", "failed or passed an exam", "is or isn't a lawyer", and many more might be the attributes. The population is sampled without replacement. That means the draws cannot be independent: each draw will affect the next one. That's why, if there is any draw, it will reduce the population's size. In hypergeometric distribution, we usually have to make our selection between the two groups, and we will do this without replacing the groups' members. Suppose there are a set of N items, and we randomly choose n items without replacement. The one type of items will be shown by K (for convenience, called success), and the second type of items will be shown by N-K (for convenience called failure). In this case, the hypergeometric distribution will be described by the probability mass function of random distribution X. The hypergeometric distribution will be in the form: 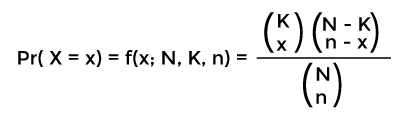
Where N is used to show the size of population. K is used to show the amount of successes in population x is used to show the amount of observed success n is used to show the amount or number of draws. We can derive the above formula by selecting the x of the K possible success in ways, after that selecting (n - x) of the (N - K) possible failures in There are a lot of similarities between the binomial distribution and hypergeometric distribution. The binomial distribution will be known as an excellent approximation of hypothesis distribution only if we are going to sample the 5% or less than 5% of the population. So we should know about the binomial distribution as well as the formula of combination to understand the hypergeometric distribution. Suppose we have a collection of 50 bulbs in which 5 bulbs are defective, and 45 bulbs are fine. The hypergeometric distribution is a type of probability distribution in which we will randomly sample 4 bulbs in the set of 50 bulbs without replacing the bulbs. While the binomial distribution is also a type of probability distribution in which we will sample 4 bulbs with replacement of the defective bulbs. The binomial distribution will be useful in the case where observed information cannot re-occur. For example, the card game or poker game where observance of the card implies that a card which we draw cannot come again in our hand. The binomial distribution is also useful in a lot of the same situations like it is used to include statistical significance and risk management. Examples of Hypergeometric DistributionExample 1: In this example, we will assume that we are playing a card game with the help of an ordinary deck. Suppose we randomly choose 5 cards from the deck without replacement. We have to find out the probability of getting exactly 2 red cards that can be either hearts or diamonds. Solution: This example is a hypergeometric experiment, and it contains the following values: N = 52, because a deck contains total 52 cards. K = 26, because a deck contains total 26 red cards. n = 5, because the randomly chosen card from the deck is 5. x = 2, because we choose 2 red cards. When we put these values into the hypergeometric distribution, we will get the following value: 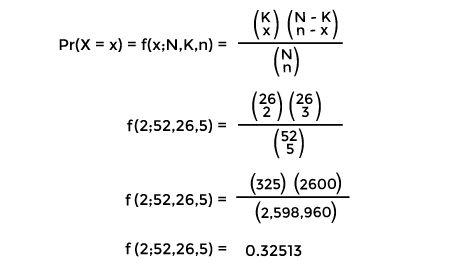
So we can say that 0.32513 is the probability of randomly choosing 2 red cards. Example 2: Suppose there are 21 balls in a bag, and in which there are 13 orange and 8 green balls. We have to determine the resulting hypergeometric distribution if we draw 5 balls from the bag. Solution: In this example, the total size of population is 13 + 8 = 21. Here we have 13 objects with desired attribute (orange) and 5 draws. So, N = 52, because a bag contains total 21 cards. K = 13, because a bag contains total 13 orange balls. n = 5, because 5 balls is drawn from the bag. x = 0, 1, 2, 3, 4, 5 When we put these values into the formula of hypergeometric distribution, we will get the following value: 
Properties of Hypergeometric DistributionHere we will describe the various important values that are used to provide the information related to the hypergeometric distribution, which is described as follows:
The mean, mode, and variance are mostly used in the hypergeometric distribution, but the mode is not generally used.
Next TopicRegular Grammar in Discrete Mathematics
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





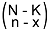 , and lastly accounting for the total
, and lastly accounting for the total 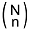 possible n-person draws.
possible n-person draws.




