Binary Search TreesBinary search trees have the property that the node to the left contains a smaller value than the node pointing to it and the node to the right contains a larger value than the node pointing to it. It is not necessary that a node in a 'Binary Search Tree' point to the nodes whose value immediately precede and follow it. Example: The tree shown in fig is a binary search tree. 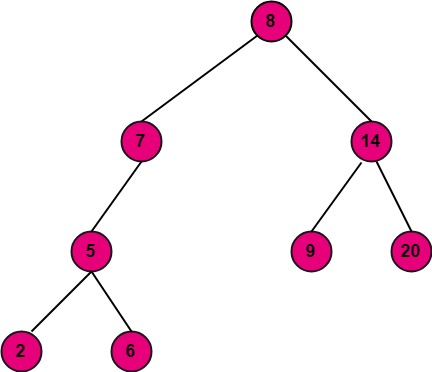
Inserting into a Binary Search Tree: Consider a binary tree T. Suppose we have given an ITEM of information to insert in T. The ITEM is inserted as a leaf in the tree. The following steps explain a procedure to insert an ITEM in the binary search tree T.
Example: Show the binary search tree after inserting 3, 1,4,6,9,2,5,7 into an initially empty binary search tree. Solution: The insertion of the above nodes in the empty binary search tree is shown in fig: 
Deletion in a Binary Search Tree: Consider a binary tree T. Suppose we want to delete a given ITEM from binary search tree. To delete an ITEM from a binary search tree we have three cases, depending upon the number of children of the deleted node.
Example: Show that the binary tree shown in fig (viii) after deleting the root node. Solution: To delete the root node, first replace the root node with the closest elements of the root. For this, first, move one step left and then to the right as far as possible to the node.Then delete the replaced node. The tree after deletion shown in fig: 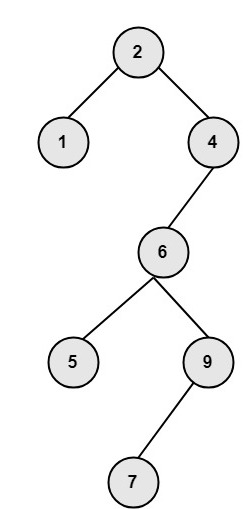
Next TopicMinimum Spanning Tree
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










