Linear Function in Discrete mathematics

A linear function can be described as a function that shows a straight line on the coordinate plane. Suppose there is a function y = 3x - 2, which shows a straight line on a coordinate plane. Hence this function is also a linear function. Since, we can replace y with f(x). So we can use another way to write this function, i.e., f(x) = 3x+2. In this section, we will learn about the definition, graph, domain, and range of the linear function. After that, we will learn to identify a linear function and find its inverse.

Definition of Linear function

A linear function can be described as a function, which must be in the form f(x) = mx+b. In this equation, m and b are used to indicate the real numbers. This equation looks the same as the slope-intercept equation from a line, which is y = mx+b. They look similar because a linear function is used to represent a line. That means the graph of this function is a line. Here

'm' is used to indicate the slope of a line

'b' is used to indicate the y intercept of a line

'x' is used to indicate the independent variable.

f(x) or 'y' is used to indicate the dependent variable.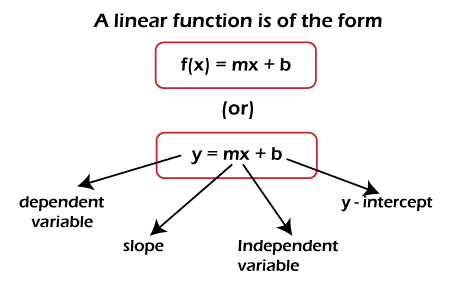

A linear function can be described as an algebraic function.

Example and Equation of Linear function

The parent linear function is indicated by f(x) = x, which is actually a line passing through the origin. In general, the equation of linear function is indicated as f(x) = mx + b. Some examples of linear function are described as follows:

f(x) = 6x-5.

f(x) = -7x - 0.7

f(x) = 4

Real-life example of Linear function

We can also explain the linear function with the help of some real-life applications, which are described as follows:

• Suppose there is a movie streaming company that charges a monthly fee approx 500rs, and for every movie downloaded, they also charge an additional fee of 30rs. In this case, the linear function will be used to represent the total monthly fee as f(x) = 30x + 500. Here x is used to show the number of movies that we have downloaded in a month.
• Suppose there is a t-shirt company that prints designs and logos on t-shirts, and that company charges a one-time fee of 3800 and 500 per t-shirt. Now we can use the linear function to show the total fee as f(x) = 500x + 3800. Here x is used to indicate the number of t-shirts.
• In linear programming problems, we can use the linear function because it represents an objective function. This function will help to maximize the profits and minimize the close.

Finding of Linear function

We can find the linear function with the help of either point-slope form or the slope-intercept form. The process of determining a linear function and determining the equation of a line is similar, and we will explain this with the help of following example.

Example: In this example, we have to determine the linear function, which contains two functions (-1, 15) and (2, 27).

Solution: From the question, we have two points, i.e., (x₁, y₁) = (-1, 15), and (x₂, y₂) = (2, 27).

Step 1: In this step, we will use the slope formula to determine the slope of the function like this:

M = (y₂-y₁) / (x₂-x₁) = (27-15) / (2-(-1)) = 12 /3 = 4.

Step 2: In this step, we will use the point slope form so that we can find out the equation of linear function like this:

y - y₁= m(x - x1)

y-15 = 4(x-(-1))

y-15 = 4(x+1)

y-15 = 4x+4

y = 4x+19

Therefore, the linear function equation is f(x) = 4x + 19.

Identifying a Linear function

If we get the information about a function in the form of a graph, and that graph is a line, then that function will be a linear function. If we get information about a function in the form of algebraic, which is in the form f(x) = mx+b, then that function will also be a linear function. If we want to check that the given data, which is represented in the table format, represents a linear function, then we can do this with the help of following steps:

• We will calculate the differences in x values
• Then, we will calculate the differences in y values
• Lastly, we will see whether the ratio of differences in y values to the differences of x values always be a constant.

Example: In this example, we have some data in the table, and we have to show whether this data represents a linear function.

Solution: To do this, we will calculate the differences in x values, y values, and ratio (difference in y) / (difference in x) every time, and from these calculations, we will see whether the ratio is a constant.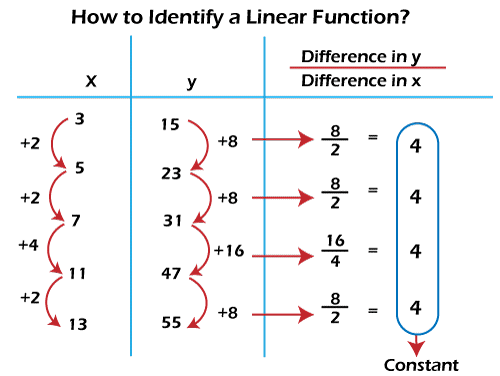

Graphing a Linear function

As we know that we can graph a line with the help of any two points on it. When we are able to find those two points, then we need to just join them in a line and then extend them on both sides. The following things are contained by the graph of a linear function f(x) = mx+b

When m>0, in this case, the graph will be an increasing line.

When m<0, in this case, the graph will be a decreasing line

When m<0, in this case, the graph will be a decreasing line.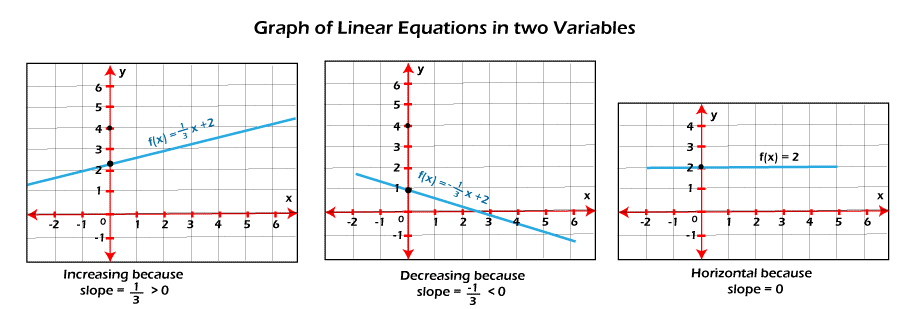

• We can determine two points on it.
• We can use the y-intercept and its slope.

Graphing a Linear function by finding two points

We will use the function f(x) = mx+b so that we can determine the two points on it. To do this, we will take some random values for x and find the corresponding value of y with the help of substituting these values on the function f(x). Now we will explain the process of graph a function with the help of an example in which we will graph a function f(x) = 3x + 5 like this:

Step 1: In this step, we will use some random values to determine the two points on the line. So we will take two points as x = -1, and x = 0.

Step 2: Now, we will find the corresponding y values with the help of substituting the above values of x in the function.

In the following table, we can see the linear function y = 3x+5 like this:

Therefore, (-1, 2) and (0, 5) are two points on the line.

Step 3: Now, we will plot these points on the graph and use a line to join them. We will also extend the line on left side and right side like this: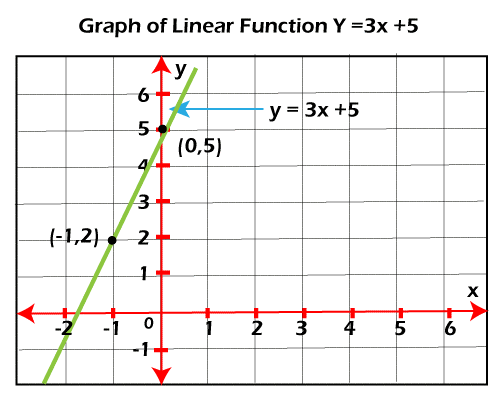

Graphing a Linear function using y-intercept and slope

With the help of the y-intercept 'b' and slope 'm' of a linear function f(x) = mx+b, we can graph any function. Now we will explain the process to do this by again using the same linear function f(x) = 3x+5. The (0, b) = (0, 5) is used to show the y-intercept of this function, and m = 3 is used to show its slope. The steps/process to do this is described as follows:

Step 1: In this step, we will plot the y-intercept (0, b), which is equal to (0, 5). So we will plot the points (0, 5).

Step 2: Now, we have to write the slope in the form of a fraction rise/run and then find out the "rise" and "run".

Here slope = 3 = 3/1 = rise/run

So rise = 3, and run = 1.

Step 3: In this step, we will get the new points by rising y-intercepts vertically with the help of "rise" and then run horizontally with the help of "run".

Note: The graph will go up if the "rise" is positive, and the graph will go down if the "rise" is negative. Similarly, we will go right if the "run" is positive, and we will go left if the "run" is negative.

In this graph, we will go up by 3 units from y-intercept and thereby go right by 1 unit.

Step 4: Now, we will use a line to join the points from step 1 to step 2, and extend those lines on both sides.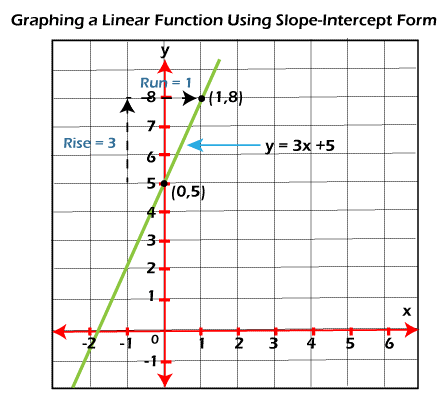

Domain and Range of a Linear function

A set of all real numbers is contained by the range and domain of a linear function. In the below image, we can see f(x) = 2x+3 and g(x) = 4-x both functions are plotted on the same axes like this: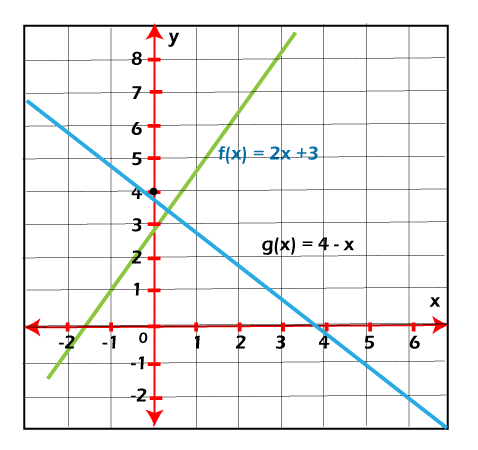

Here R is used to show the domain of a linear function, and R is also used to show the range of a linear function.

Note:

1. If the problem does not contain any specific range or domain, only then the domain and range of a linear function will be R.
2. The horizontal line will be shown by the linear function f(x) = b if the slope m = 0. In this case, the range of this function = {b} and the domain of this function = R.

Inverse of a Linear function

The function f^-1(x) is used to indicate the inverse of a linear function f(x) = ax+b in such a way that f(f^-1(x)) = f^-1(f(x)) = x. Now we will use an example to show the process to identify the inverse of a linear function. In this example, we have a linear function f(x) = 3x+5, and we will find the inverse of this function.

Step 1: In the first step, we will replace f(x) with y. By replacing, we will get the following equation:

y = 3x+5

Step 2: Now, we will interchange the variables x and y and get the following equation:

x = 3y+5

Step 3: Now we will solve the above equation for y like this:

x-5 = 3y

y = (x-5) /3

Step 4: Now we will replace y by inverse function f^-1(x), and get the following:

f^-1(x) = (x-5) /3

Note that the function f(x) and the inverse function f^-1(x) are always symmetric with respect to line y = x. Now we will plot the linear function f(x) and its inverse function f^-1(x). Here f(x) = 3x+5 and f^-1(x) = (x-5)/3. Here we will check whether these functions are symmetric about y = x, and we will also see when (x, y) lies on f(x), then (y, x) lies on f^-1(x). To prove this, we will take an example in which we have (-1, 2), which lies on f(x), and (-2, 1), which lies on f^-1(x). The graphical representation of all these things is described as follows: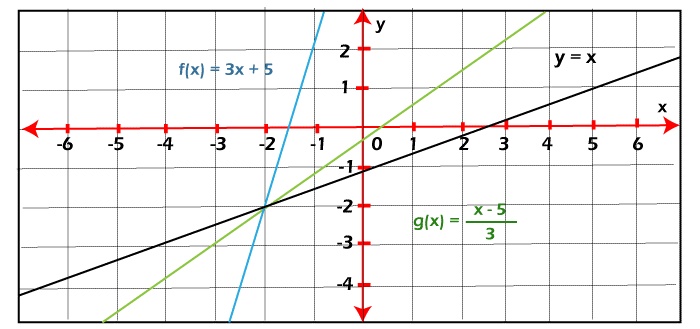

Piecewise Linear function

There are some cases where the linear function is defined in a uniform way throughout its domain. This is because its domain can be split into two or more than two parts, so the linear function can be defined in two or more than two ways in some cases. This type of linear function is known as the piecewise linear function. The example of a piecewise linear function is described as follows:

Example: In this example, we have a linear function, and we have to plot the graph of this function. The function f(x) is described as follows: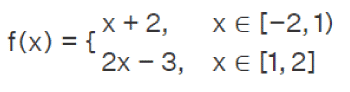

Solution: The above described piecewise function is linear in both the above described parts of its domain. Now we will determine the endpoint of the line by taking both the cases.

When the case is x ∈ [-2, 1):

When x ∈ [1, 2):

The corresponding graph is described as follows: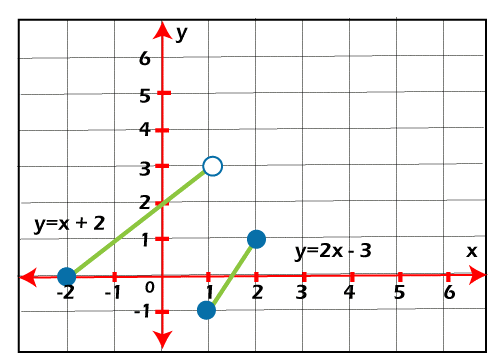

Important notes

• If a linear function must be in the form f(x) = mx+b, then the graph of this function will be a line.
• When the slope of the linear function f(x) = mx+b is 0, the linear function will be a horizontal line, and this function will be known as the constant function.
• In a linear function f(x) = ax+b, the domain and range will be R. Whereas for a constant function f(x) = b, the range will be {b}.
• We can use these linear functions in linear programming to show the objective function.
• There is no inverse in a constant function because this function is not one to one.
• If the slopes of the two linear functions are equal, then both functions will be parallel.
• If the product of slopes of two linear functions is -1, then both the functions will be perpendicular.
  The linear function fails the test of a vertical line. That's why the vertical line is not a linear function.