Problems based on Converse, inverse and Contrapositive

If we want to learn the converse, inverse, and contrapositive statements, we have to see our previous article, Logical Connectives.

Logical Connectives

Logical connectives are a type of operator which is used to combine one or more than one propositions. There are basically 5 types of connectives in propositional logic. In this section, we are going to learn about the converse, inverse, and contrapositive of conditional statements.

Converse, Inverse and Contrapositive

If there is a conditional statement x → y, then

• The converse statement will be y → x
• The inverse statement will be ∼x → ∼y
• The contrapositive statement will be ∼y → ∼x

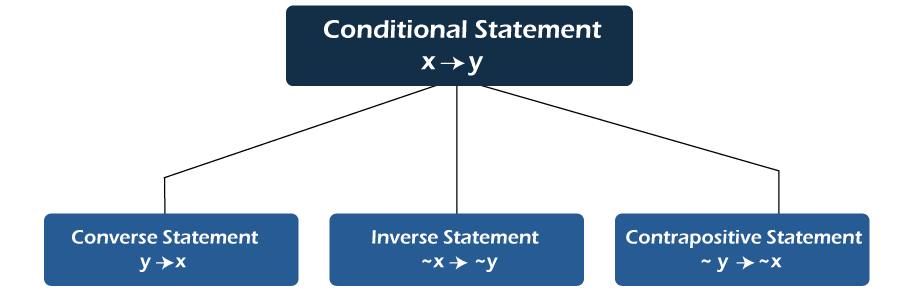
Important Notes:

There are some important points that we should keep in our mind, which are described as follows:

Note 1: We can only write the converse, inverse, and contrapositive statements only for the conditional statements x → y.

Note 2: If we perform two actions, then the output will always be the third one.

For example:

• Contrapositive can be described as a inverse of converse.
• Converse can be described as an inverse of contrapositive.
• Contrapositive can be described as a converse of inverse.
• Inverse can be described as a converse of contrapositive.
• Converse can be described as a contrapositive of inverse.
• Inverse can be described as a contrapositive of converse.

Note 3:

For a conditional statement x → y,

There will be an equal result between its converse statement (y → x) and the inverse statement (∼x → ∼y).

There will also be the same result between x → y and its contrapositive statement (∼y → ∼x).

Problem-based on Converse, Inverse and Contrapositive

There are some problems on the basis of the converse, inverse, and contrapositive, and we will show some of them like this:

Problem 1:

Here we will write the converse, inverse, and contrapositive of some statements, which are shown below:

1. If the weather is sunny, then I will go to school.
2. If 3y - 2 = 10, then x = 1.
3. If there is rainy weather, then I will go outside to enjoy it.
4. You will get good marks only if you study hard.
5. I will go to the market if my cousins come.
6. I go to college whenever my friends come.
7. I will give you a party only if I buy a good dress.
8. If I become famous, then I will earn a lot of money.

Solution:

Part 1:

We have the following details:

The given statement is, "If the weather is sunny, then I will go to school."

This statement must have the form: "if x then y".

So, this statement contains a symbolic form, i.e., x → y, where

x: The weather is sunny

y: I will go to school

Converse Statement: If I will go to school, then the weather is sunny.

Inverse Statement: If the weather is not sunny, then I will not go to school.

Contrapositive Statement: If I will not go to school, then the weather is not sunny.

Part 2:

We have the following details:

The given statement is, "If 3a - 2 = 10, then a = 1."

This statement must have the form: "if x then y".

So, this statement contains a symbolic form, i.e., x → y, where

x: 3a - 2 = 10

y: a = 1

Converse Statement: If a = 1, then 3a - 2 = 10.

Inverse Statement: If 3a - 2 ≠ 10, then a ≠ 1.

Contrapositive Statement: If a ≠ 1, then 3a - 2 ≠ 10.

Part 3:

We have the following details:

The given statement is, "If there is rainy weather, then I will go outside to enjoy it."

This statement must have the form: "if x then y".

So, this statement contains a symbolic form, i.e., x → y, where

X: There is rainy weather

Y: I will go outside to enjoy it

Converse Statement: If I will go outside to enjoy it, then there is rainy weather.

Inverse Statement: If there is no rainy weather, then I will not go outside to enjoy it.

Contrapositive Statement: If I will not go outside to enjoy it, then there is no rainy weather.

Part 4:

We have the following details:

The given statement is, "You will get good marks only if you study hard."

This statement must have the form: "x only if y".

So, this statement contains a symbolic form, i.e., x → y, where

X: You will get good marks

Y: You study hard

Converse Statement: If you study hard, then you will get good marks.

Inverse Statement: If you do not get good marks, then you do not study hard.

Contrapositive Statement: If you do not study hard, then you will not get good marks.

Part 5:

We have the following details:

The given statement is, "I will go to the market if my cousins come."

This statement must have the form: "y if x".

So, this statement contains a symbolic form, i.e., x → y, where

X: My cousins come

Y: I will go to the market

Converse Statement: If I will go to the market, then my cousins come.

Inverse Statement: If my cousins do not come, then I will not go to the market.

Contrapositive Statement: If I will not go to the market, then my cousins do not come.

Part 6:

We have the following details:

The given statement is, "I go to college whenever my friends come."

In this statement, "whenever" can be replaced with "if".

After replacing the sentence will be - "I go to college if my friends come"

So, this statement contains a symbolic form, i.e., x → y, where

X: My friends come

Y: I go to college

Converse Statement: If I go to college, then my friends come.

Inverse Statement: If my friends do not come, then I will not go to college.

Contrapositive Statement: If I do not go to college, then my friends do not come.

Part 7:

We have the following details:

The given statement is, "I will give you a party only if I buy a good dress."

This statement must have the form: "x only if y".

So, this statement contains a symbolic form, i.e., x → y, where

X: I will give you a party only

Y: I buy a good dress

Converse Statement: If I buy a good dress, then I will give you a party.

Inverse Statement: If I will not give you a party, I do not buy a good dress.

Contrapositive Statement: If I do not buy a good dress, then I will not give you a party.

Part 8:

We have the following details:

The given statement is, "If I become famous, then I will earn a lot of money."

This statement must have the form: "If x then y".

So, this statement contains a symbolic form, i.e., x → y, where

X: I become famous

Y: I will earn a lot of money

Converse Statement: If I earn a lot of money, then I become famous.

Inverse Statement: If I do not become famous, then I will not earn a lot of money.

Contrapositive Statement: If I do not earn a lot of money, then I will not become famous.

Problem 2:

Here we have to determine the converse a statement, i.e., "I go to school only if the weather is sunny" among all the given statements.

1. I go to school if the weather is sunny
2. If I go to school, then the weather is sunny
3. If the weather is not sunny, then I do not go to school.
4. If I do not go to school, then the weather is sunny.

Solution:

We have the following details:

The given statement is, "I go to school only if the weather is sunny."

This statement must have the form: "x only if y". We can also write it as "If x then y".

So, this statement contains a symbolic form, i.e., x → y. The converse of this form will be y → x, where

X: I go to school

Y: The weather is sunny

As we know that the converse statement of the given statement will be "If the weather is sunny, then I go to school", which is in the form "if y then x".

• The first statement is true. The first statement is, "I go to school if the weather is sunny". This statement is in the form "x if y". We can also write it as "if x then y", which indicates that "If the weather is sunny, then I go to school", which is the converse of a given statement. That's why the first statement is true.
• The second statement is false. The second statement is, "If I go to school, then the weather is sunny" and this statement is in the form "if x then y". The second statement is already given in the question. That's why it is not true.
• The third statement is false. The third statement is, "If the weather is not sunny, then I do not go to school". This statement is in the form "∼y → ∼x". It is not the converse because this statement is the inverse of statement given in the question. That's why this statement is not true.
• The fourth statement is false. The fourth statement is, "If I do not go to school, then the weather is sunny". This statement is in the form "∼x → y. This form is something different because it is neither inverse nor converse nor contrapositive. This is because one side is negative, and the other side is not negative, so it will not fit in any of the categories. That's why this statement is not true.

Hence, option (A) is true.