Functions

It is a mapping in which every element of set A is uniquely associated at the element with set B. The set of A is called Domain of a function and set of B is called Co domain.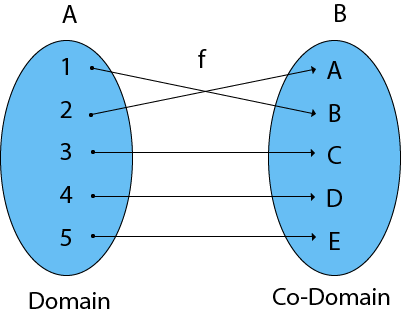

Domain, Co-Domain, and Range of a Function:

Domain of a Function: Let f be a function from P to Q. The set P is called the domain of the function f.

Co-Domain of a Function: Let f be a function from P to Q. The set Q is called Co-domain of the function f.

Range of a Function: The range of a function is the set of picture of its domain. In other words, we can say it is a subset of its co-domain. It is denoted as f (domain).

If f: P → Q, then f (P) = {f(x): x ∈ P} = {y: y ∈ Q | ∃ x ∈ P, such that f (x) = y}.

Example: Find the Domain, Co-Domain, and Range of function.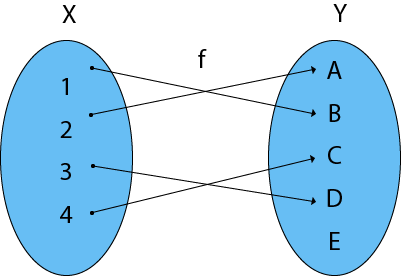

Let x = {1, 2, 3, 4}
    y = {a, b, c, d, e}
    f = {(1, b), (2, a), (3, d), (4, c)

Solution:

Domain of function: {1, 2, 3, 4}
Range of function: {a, b, c, d}
Co-Domain of function: {a, b, c, d, e}

Functions as a Set

If P and Q are two non-empty sets, then a function f from P to Q is a subset of P x Q, with two important restrictions

∀ a ∈ P, (a, b) ∈ f for some b ∈ Q
If (a, b) ∈ f and (a, c) ∈ f then b = c.

Note1: There may be some elements of the Q which are not related to any element of set P.

2. Every element of P must be related with at least one element of Q.

Example1: If a set A has n elements, how many functions are there from A to A?

Solution: If a set A has n elements, then there are nⁿ functions from A to A.

Representation of a Function

The two sets P and Q are represented by two circles. The function f: P → Q is represented by a collection of arrows joining the points which represent the elements of P and corresponds elements of Q

Example1:

Let  X = {a, b, c} 	and Y = {x, y, z}   and f: X → Y such that
     f= {(a, x), (b, z), (c, x)}

Then f can be represented diagrammatically as follows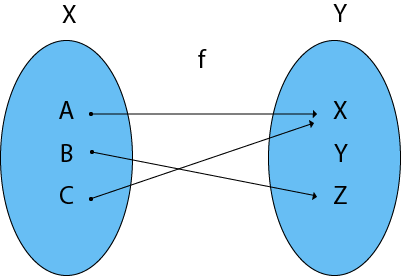

Example2: Let X = {x, y, z, k} and Y = {1, 2, 3, 4}. Determine which of the following functions. Give reasons if it is not. Find range if it is a function.

f = {(x, 1), (y, 2), (z, 3), (k, 4)
g = {(x, 1), (y, 1), (k, 4)
h = {(x, 1), (x, 2), (x, 3), (x, 4)
l = {(x, 1), (y, 1), (z, 1), (k, 1)}
d = {(x, 1), (y, 2), (y, 3), (z, 4), (z, 4)}.

Solution:

It is a function. Range (f) = {1, 2, 3, 4}
It is not a function because every element of X does not relate with some element of Y i.e., Z is not related with any element of Y.
h is not a function because h (x) = {1, 2, 3, 4} i.e., element x has more than one image in set Y.
d is not a function because d (y) = {2, 3} i.e., element y has more than image in set Y.

Next TopicTypes of Functions

← prev next →