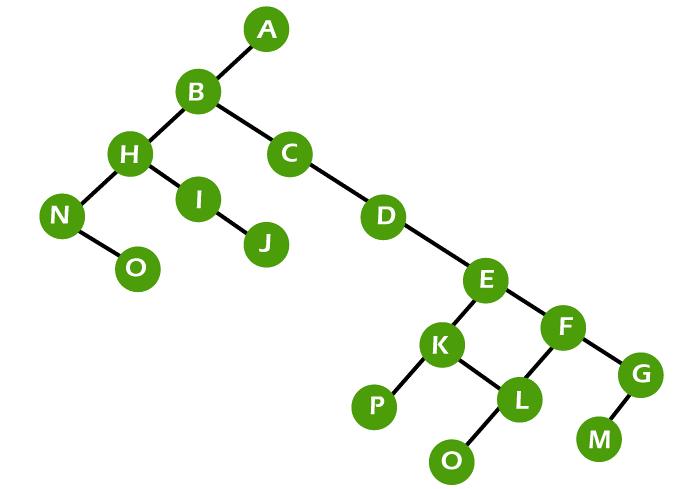
M-array Tree in Discrete MathematicsAn m-array tree can be described as a generalization of a binary tree in which each and every node has M or less children. In other words, a tree will be known as the m array tree if each node of the tree does not contain more than m children. A binary tree will be known as the M-ary tree if it contains M = 2. With the help of following image, we can see an example of M-ary tree where M = 3. 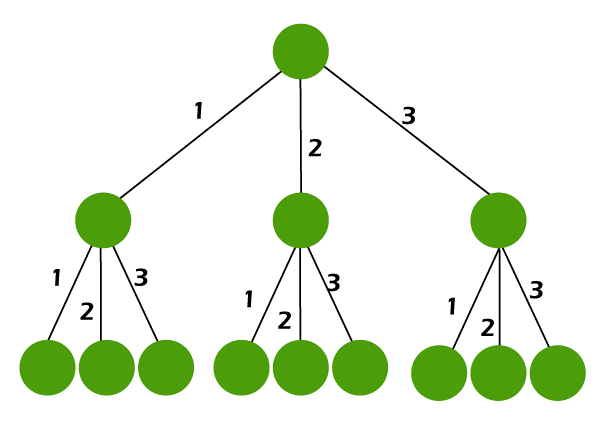
Types of M-ary tree
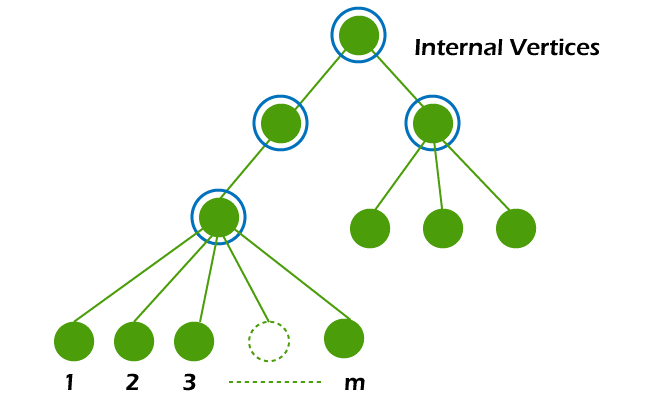
Properties of M-ary treeThere are various properties in m ary tree, and some of them are described as follows: If there is a full m ary tree, which has i internal vertices, then we can calculate the vertices and leaves of that tree with the help of following formula: 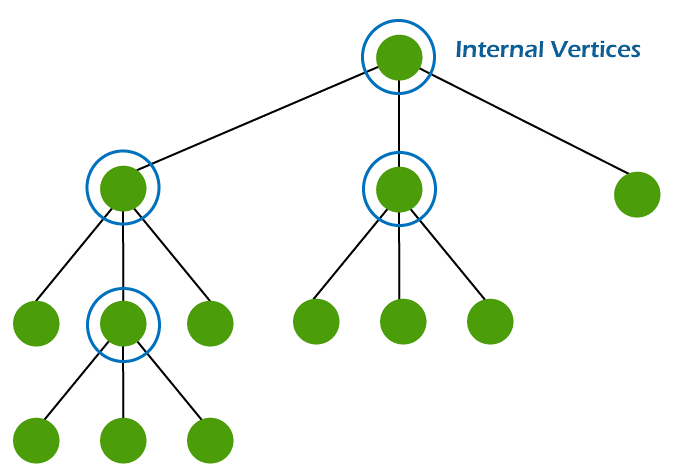
For example: Suppose there are 4 internal vertices and m = 3 in a tree. Now we have to calculate the number of vertices and number of leaves in that tree. Solution: From the question, we have m = 3, and i = 4 and we know that Among 13 vertices, there is a root vertice, and the remaining 12 vertices are children of those 4 internal vertices. Now we will calculate the leaves of the tree with the help of following formula: Hence there will be 13 vertices and 9 numbers of leaves. TraversalThe binary trees and the M ary tree both have the same properties, which are described as follows: Pre-order traversal: In the process of pre-order traversal, we will first visit a root node, and then we will traverse to its subtree, which contains the left subtree and the right subtree. So after visiting the root node, we will first traverse the left subtree, and then we will traverse the right subtree. We can only visit one node at a time. The name "preorder traverse" also refers to the root node coming before the left and right subtree. In the preorder traverse, the time complexity is O(n). In the following form, we can represent the process of preorder traversal like this: Post-order traversal: In the process of post-order traversal, we will follow the left-right root policy. In this policy, we will recursively traverse all subtrees rooted in children. There are two subtrees: the left subtree and right subtree. So we will first traverse the left subtree, and then we will traverse the right subtree. Only after visiting all subtrees, we will visit the root. The name "post-order traverse" also refers to the root node coming after the left and right subtree. In the post-order traversal, the time complexity is also O(n). In the following form, we can represent the process of post-order traversal like this: In order traverse: In the process of in-order traversal, we will follow the left-root-right policy. In this policy, we will first traverse the left subtrees, then we will visit the root, and after that, we will traverse the right subtree. The name "in-order traverse" also refers to the root node will come between the left and right subtree. In in-order traversal, the time complexity is also O(n). In the following form, we can represent the process of in order traverse like this: There is one more way in which we can explain the traversal of m ary tree. The traversal of binary tree and the m ary tree are both similar. But there can be a case where m>2, which contains more than two children per node, so we have to define the notation of left and right subtrees. We can get the left and right subtree with the help of dividing the list of children nodes of the tree into two groups. With the help of defining the order on the m children of a node, we will constitute some part of the node on the left subtree, i.e., {0, 1,... m/2}, and we will constitute the other part of the node on the right subtree, i.e., {m/2, ...., m}. 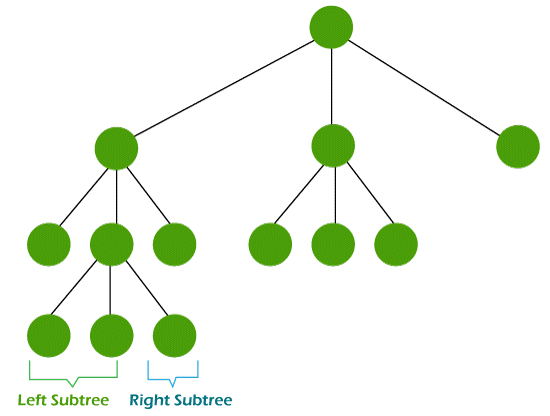
Method of storing m-ary treesWe can store the m ary tree with the help of two ways: we can use an array, or we can use a pointer-based. Now we will explain them one by one like this: Array: Suppose we have a complete m ary tree. In this type of compact arrangement, if there is an index i, then we can find its cth child in range {1,...., m} with the help of its index m.i + c. In this case, this method wastes no space. In this type of method, the space complexity will be O(mn). 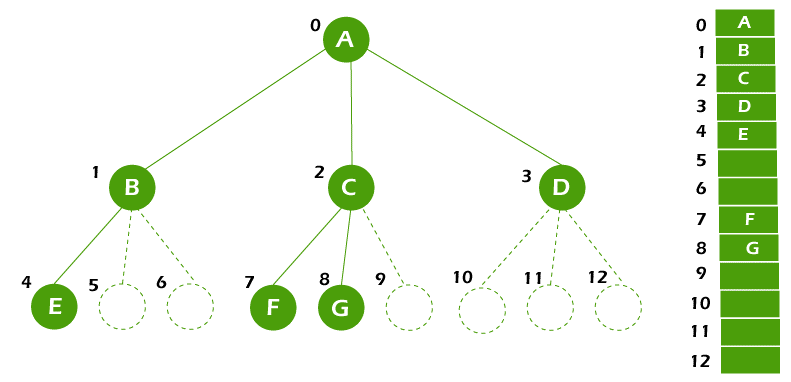
Pointer-based: There must be an internal array for each node so that this array can store pointers to each of its m children. The implementation method of pointer-based contains superior space complexity as compared to the array-based implementation. So the space complexity of pointer-based method is O(m.n). 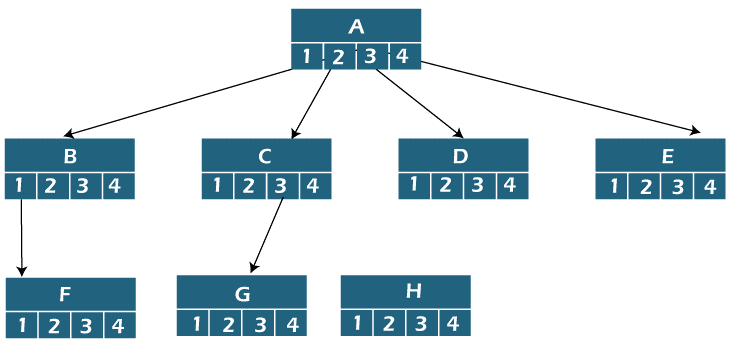
Converting m-ary tree into binary treeSuppose we try to convert an arbitrary m ary tree into a binary tree. In this case, we have to use a constant factor, which is used to only increase the height of a tree, and it will not be useful to affect the overall worst-case time complexity. First, we will form a link list with the help of linking all the intermediate children nodes of the given parent node. After that, we will keep the link from parent to the first child, i.e., the leftmost child, and in this process, we will remove all the other links to the rest children. 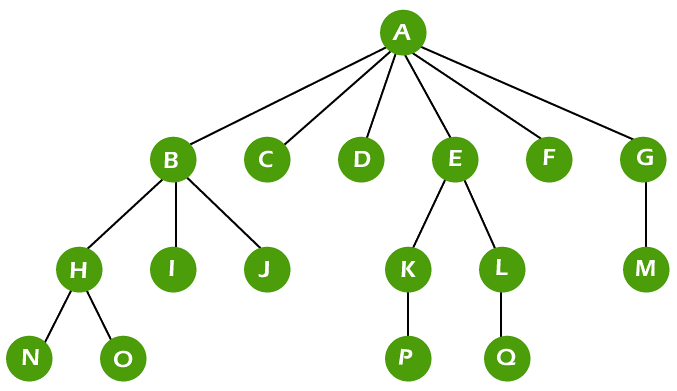
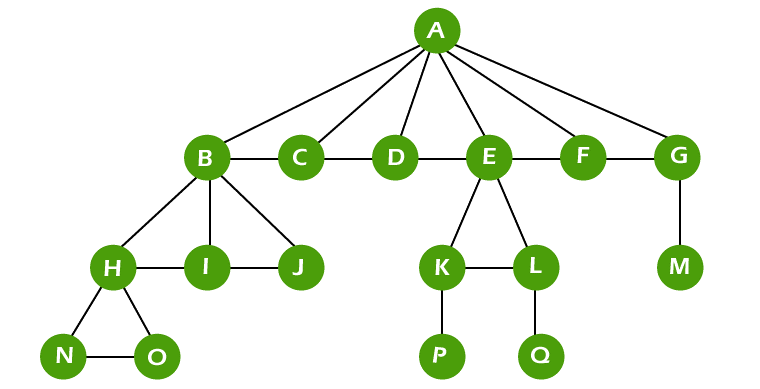
↓ 
↓ 
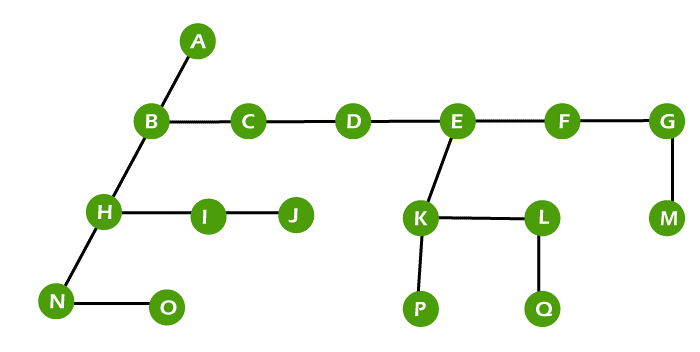
↓ 
Applications of M-ary treesThere are a lot of applications in the M-ary tree, and some of them are described as follows:
In the following image, we will indicate an example of a grammar tree like this: 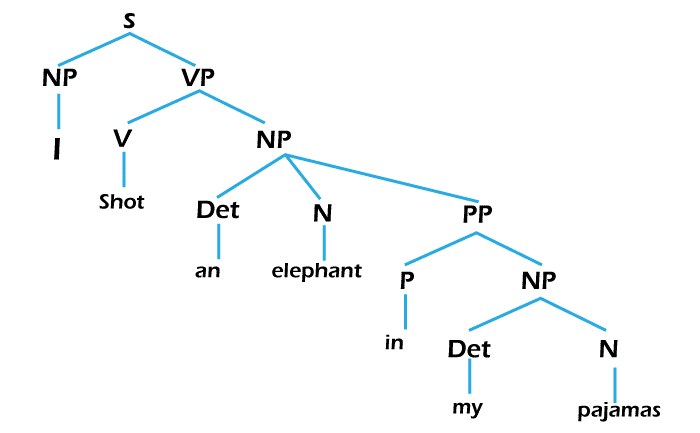
Next TopicMatrix in Discrete mathematics
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









