Handshaking Theory in Discrete mathematics

We can also call the handshaking theory as the Sum of degree theorem or Handshaking Lemma. The handshaking theory states that the sum of degree of all the vertices for a graph will be double the number of edges contained by that graph. The symbolic representation of handshaking theory is described as follows:

Here,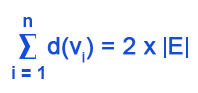

Handshaking Theory in Discrete mathematics

'd' is used to indicate the degree of the vertex.

'v' is used to indicate the vertex.

'e' is used to indicate the edges.

Handshaking Theorem:

There are some conclusions in the handshaking theorem, which must be drawn, which are described as follows:

In any graph:

There must be even numbers for the sum of degree of all the vertices.
If there are odd degrees for all the vertices, then the sum of degree of these vertices must always remain even.
If there are some vertices that have an odd degree, then the number of these vertices will be even.

Examples of Handshaking theory

There are various examples of handshaking theory, and some of the examples are described as follows:

Example 1: Here, we have a graph that has the degree of each vertex as 4 and 24 edges. Now we will find out the number of vertices in this graph.

Solution: With the help of above graph, we have got the following details:

Degree of each vertex = 24

Number of edges = 24

Now we will assume the number of vertices = n

With the help of Handshaking theorem, we have the following things:

Sum of a degree of all Vertices = 2 * Number of edges

Now we will put the given values into the above handshaking formula:

n*4 = 2*24

n = 2*6

n = 12

Thus, in graph G, the number of vertices = 12.

Example 2: Here, we have a graph that has 21 edges, 3 vertices of degree 4, and all other vertices of degree 2. Now we will find out the total number of vertices in this graph.

Solution: With the help of above graph, we have got the following details:

Number of Degree 4 vertices = 3

Number of edges = 21

All other vertices have degree 2

Now we will assume the number of vertices = n

With the help of Handshaking theorem, we have the following things:

Sum of degree of all Vertices = 2 * Number of edges

Now we will put the given values into the above handshaking formula:

3*4 + (n-3) * 2 = 2*21

12+2n-6 = 42

2n = 42 - 6

2n = 36

n = 18

Thus, in graph G, the total number of vertices = 18.

Example 3: Here, we have a graph that has 35 edges, 4 vertices of degree 5, 5 vertices of degree 4, and 4 vertices of degree 3. Now we will find out the number of vertices with degree 2 in this graph.

Solution: With the help of above graph, we have got the following details:

Number of edges = 35

Number of Degree 5 vertices = 4

Number of degree 4 vertices = 5

Number of degree 3 vertices = 4

Now we will assume the number of degree 2 vertices = n

With the help of Handshaking theorem, we have the following things:

Sum of degree of all Vertices = 2 * Number of edges

Now we will put the given values into the above handshaking formula:

4*5 + 5*4 + 4*3 + n*2 = 2*35

20 + 20 + 12 + 2n = 70

52+2n = 70

2n = 70-52

2n = 18

n = 9

Thus, in graph G, number of degree 2 vertices = 9.

Example 4: Here, we have a graph that has 24 edges, and the degree of each vertex is k. Now we will find out the possible number of vertices from the given options.

Solution: With the help of above graph, we have got the following details:

Number of edges = 24

Degree of each vertex = k

Now we will assume the number of vertices = n

With the help of Handshaking theorem, we have the following things:

Sum of degree of all Vertices = 2 * Number of edges

Now we will put the given values into the above handshaking formula:

N*k = 2*24

K = 48/n

It is mandatory that a whole number is contained by the degree of any vertex.

So we can use only those types of values of n in the above equation that provides us a whole value of k.

Now, we will check the above given options by putting them in the place of n one by one like this: