Row matrix in Discrete mathematicsA matrix will be known as a row matrix if it contains only one row. But there can be more than one element in the column in case of a row matrix. With the help of order 1∗n, we can indicate the order of row matrix. Here 1 is used to indicate the number of rows, and n is the number of columns. In any matrix, the rows and columns are used to contain the elements. We can indicate the row elements with the help of horizontal arrangement. Suppose there is a matrix B = [bij], which contains an order 1∗n. The row matrix will be indicated as follows:
[bij]1∗n is a row matrix
For example: X = [4 6]1∗2 Y = [x y z]1∗3 Z = [4 6 1 9]1∗4 In this section, we will learn about row matrices, their definition, properties, operations, and examples of row matrices. What is Row matrixA row matrix is a type of matrix in which all the elements are arranged in a single row. That means in a row matrix, there can be more than one column but only a single row. Suppose there is a matrix m∗n where m is used to indicate the number of rows and n is used to indicate the number of columns. In this order, if m = 1, then this type of matrix will be known as the row matrix. Thus, we can form a row matrix with the help of a horizontal line of elements. A row matrix can be described as a rectangular array of elements that are arranged in the form of a horizontal line. In the following way, we can indicate the general representation of the row matrix:
Row matrix, A = [b11 b12 b13 b14 .... b1n]1∗n
In other words, we can write it in the following way:
Row matrix = [bij]1∗n
We cannot define the determinant of row matrix because the row matrix is not a square matrix. If the order of a matrix is 1∗1, that means the number of rows and columns is 1, only then we can find the determinant of a row matrix. We cannot define the determinant of a row matrix if there is an order 1∗n where the value of n is greater than 1. Now we will show some examples so that we can better understand the concept of a row matrix. Properties of Row matrixWe can deeply understand the concept of a row matrix with the help of some properties, which are described as follows:
Operations on Row matrixIn the field of discrete mathematics, there are various kinds of operations that can be performed on a row matrix, i.e., multiplication, subtraction, addition, and division. While performing the addition and subtraction operation, we can take any other matrix to do that. If there is a row matrix, then we can perform addition and subtraction operations only on any other row matrix. For the addition or subtraction operation on row matrices, the order of these matrices must be the same. The example of addition of row matrices is described as follows: A = [4 -7 1 2], B = [3 9 5 2] A+B = [4+3 (-7)+9 1+5 2+2] = [7 2 6 4] The example of subtraction of row matrices is described as follows: A = [5 8 3 1], B = [3 2 7 9] A-B = [5-3 8-2 3-7 1-9] = [2 6 -4 -8] With the help of a column matrix, we will be able to do the multiplication of a row matrix. For matrix multiplication, we have to satisfy its condition, i.e., the number of columns in the 1st matrix and the number of rows in the 2nd matrix must be similar to each other. That means in case of multiplication operation, the number of columns in the row matrix and the number of rows in the column matrix must be similar to each other. An example of the multiplication of two rectangular matrices is described as follows: 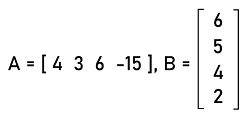
A∗B = [4∗6 + 3∗5 + 6∗4 + (-15)∗2] = [24 + 15 + 24 - 30]
= [33]
When we do the multiplication of a row matrix with the help of a column matrix, then the generated result will be a singleton matrix. If we want to do the inverse of row matrix, then it will not be possible, and because of this reason, we cannot use the row matrix for division operation. That means the row matrix can be performed on addition, subtraction, and multiplication but not on division. Examples of row matrix on the basis of orderHere we will show the row matrices with different orders, which are described as follows: Example 1: In this example, we will show a row matrix with an order 1∗1, which is described as follows: A = [7]1∗1 In this matrix, we can see that there is only 1 element, which is arranged in the form of 1 row and 1 column. In the matrix A = [7], the determinant is 7. Example 2: In this example, we will show a row matrix with an order 1∗2, which is described as follows: A = [3 7]1∗2 In this matrix, we can see that there are 2 elements, which are arranged in the form of 1 row and 2 columns. Hence we can say that it is a row matrix. Example 3: In this example, we will show a row matrix with an order 1∗3, which is described as follows: A = [4 6 8]1∗3 In this matrix, we can see that there are 3 elements, which are arranged in the form of 1 row and 3 columns. Example 4: In this example, we will show a row matrix with an order 1∗4, which is described as follows: A = [2 5 6 9]1∗4 In this matrix, we can see that there are 4 elements, which are arranged in the form of 1 row and 4 columns. Example 5: In this example, we will show a row matrix with an order 1∗5, which is described as follows: A = [1 4 7 8 3]1∗5 In this matrix, we can see that there are 5 elements, which are arranged in the form of 1 row and 5 columns. Example 6: In this example, we will show a row matrix with an order 1∗6, which is described as follows: A = [5 6 3 9 1 4]1∗6 In this matrix, we can see that there are 6 elements, which are arranged in the form of 1 row and 6 columns. All the above examples are known as row matrices because all the elements of these matrices are arranged in a single row but in more than one column. Examples of Row matricesThere are a lot of examples of row matrices, and some of them are described as follows: Example 1: In this example, we have a row matrix, and we have to transpose that matrix. The row matrix is described as follows: [3 4 1] Solution: From the question, we have a row matrix A where A = [3 4 1] We can perform the transpose of the row matrix by writing all the elements of the row matrix in the form of column elements. 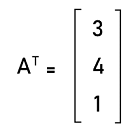
Hence, a column matrix is the transpose of the row matrix. Example 2: In this example, we have a row matrix [1 2 -1] and a column matrix, and we have to do the multiplication of both matrices. The column matrix is described as follows: 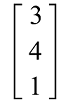
Solution: From the question, we have a row matrix and column matrix like this: 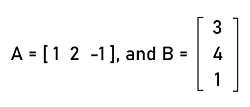
The multiplication of row matrix and column matrix is described as follows: 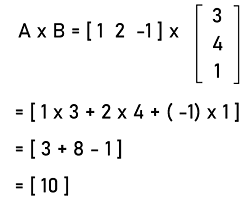
Therefore, the multiplication of row matrix and the column matrix is a singleton matrix. Important PointsThere are a lot of points that we should keep in mind while learning the concept of row matrix, which are described as follows:
Next TopicSquare matrix in discrete mathematics
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









