ProbabilityThe word 'Probability' means the chance of occurring of a particular event. It is generally possible to predict the future of an event quantitatively with a certain probability of being correct. The probability is used in such cases where the outcome of the trial is uncertain. Probability Definition:The probability of happening of an event A, denoted by P(A), is defined as 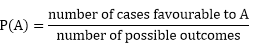
Thus, if an event can happen in m ways and fails to occur in n ways and m+n ways is equally likely to occur then the probability of happening of the event A is given by 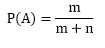
And the probability of non-happening of A is 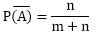
Note:
Important Terms related to Probability:1. Trial and Event: The performance of an experiment is called a trial, and the set of its outcomes is termed an event. Example: Tossing a coin and getting head is a trial. Then the event is {HT, TH, HH} 2. Random Experiment: It is an experiment in which all the possible outcomes of the experiment are known in advance. But the exact outcomes of any specific performance are not known in advance. Example:
3. Outcome: The result of a random experiment is called an Outcome. Example: 1. Tossing a coin is an experiment and getting head is called an outcome. 4. Sample Space: The set of all possible outcomes of an experiment is called sample space and is denoted by S. Example: When a die is thrown, sample space is S = {1, 2, 3, 4, 5, 6} Note1: If a die is rolled n times the total number of outcomes will be 6n.Note2: If 1 die rolled n times then n die rolled 1 time.5. Complement of Event: The set of all outcomes which are in sample space but not an event is called the complement of an event. 6. Impossible Events: An event which will never be happened. Example1: Tossing double-headed coins and getting tails in an impossible event. Example2: Rolling a die and getting number > 10 in an impossible outcome. 7. Sure Outcome/Certain Outcome: An Outcome which will definitely be happen Example1: Tossing double-headed coins and getting heads only. Example2: Rolling a die and getting number < 6 8. Possible Outcome: An outcome which is possible to occur is called Possible Outcome. Example1: Tossing a fair coin and getting a head on it. Example2: Rolling a die and getting an odd number. 9. Equally Likely Events: Events are said to be equally likely if one of them cannot be expected to occur in preference to others. In other words, it means each outcome is as likely to occur as any other outcome. Example: When a die is thrown, all the six faces, i.e., 1, 2, 3, 4, 5 and 6 are equally likely to occur. 10. Mutually Exclusive or Disjoint Events: Events are called mutually exclusive if they cannot occur simultaneously. Example: Suppose a card is drawn from a pack of cards, then the events getting a jack and getting a king are mutually exclusive because they cannot occur simultaneously. 11. Exhaustive Events: The total number of all possible outcomes of an experiment is called exhaustive events. Example: In the tossing of a coin, either head or tail may turn up. Therefore, there are two possible outcomes. Hence, there are two exhaustive events in tossing a coin. 12. Independent Events: Events A and B are said to be independent if the occurrence of any one event does not affect the occurrence of any other event. Example: A coin is tossed thrice, and all 8 outcomes are equally likely Prove that event A and B are independent. Solution: 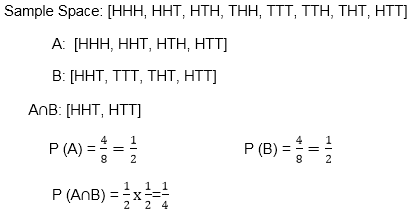
13. Dependent Event: Events are said to be dependent if occurrence of one affect the occurrence of other events.
Next TopicAddition Theorem
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









