HyperGraph & its Representation in Discrete MathematicsA hypergraph can be described as a graph where, in place of connecting with two vertices/nodes, the hypergraph is connected with a subset of vertices/nodes. The edges can also be called hyperedges, which are used to contain arbitrary non-empty sets of vertices. These types of hyperedges are contained by the k hypergraph, which is connected with exactly k vertices. If there is a normal graph, it will be known as the 2 hypergraphs because in a normal graph, one edge is connected with the 2 vertices. Representation of HypergraphAn undirected hypergraph H can be represented in a pair H = (V, E), where V is used to indicate a set of items, and these items are called vertices or nodes, and E is used to indicate a set of nonempty subsets of V, and these subsets are also called as edges or hyperedges. Here E can be defined as a subset of P(X), where P(X) is used to indicate the Power set of X. With the help of a closed curve, each hyperedge will be represented. The members of these hyperedges are contained by this closed curve so that it can create hypergraphs. For example: 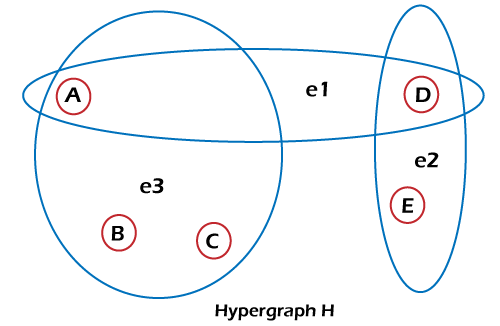
Order & Size of Hypergraph The order and size of the hypergraph can be determined with the help of following formula: Order of Hypergraph = Size of vertex set, and Size of Hypergraph = Size of the edges set So in the above hypergraph, there is a total of 5 vertices named A, B, C, D, E, and the number of edges is 3 named: e1, e2, e3. As we know, Order of hypergraph = number of vertex and size of hypergraph = number of edges. So with the help of these values, the order and size of the above hypergraph are described as follows: Hypergraph to Bi-Partite Graph With the help of bipartite, we are able to always express a hypergraph, but expressing a hypergraph with the help of a bipartite graph is not always convenient. In this process, the hypergraphs are rarely utilized. In a bipartite graph, the set of a vertex is portioned into the two subsets named P and Q. Here each edge has a connection with a vertex in P to a vertex in Q. The vertices of H can be easily represented in the form of vertices in Q. The hyperedges of H can be easily represented in the form of vertices in P. If there is a case where s is a member of hyperedge t in H, then we will insert an edge (p, q). 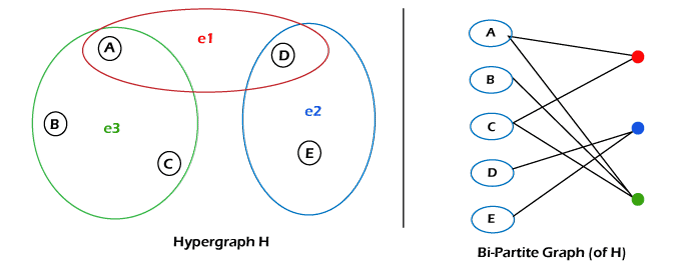
The above hypergraph is represented with the help of 2 ways. On the left side, the 5 edges are connected with the 3 hyperedges. The same 5 vertices are connected with the new vertices (three) on the right side, which is used to show the hyperedges by ordinary edges. Properties of HypergraphThere are various types of properties contained by the hypergraph, which are described as follows: Empty Hypergraph The empty hypergraph does not contain any type of edges, but it can contain vertices. Example: In the following diagram, we can see that there are no edges, but it contains five vertices named as: A, B, C, D, and E. 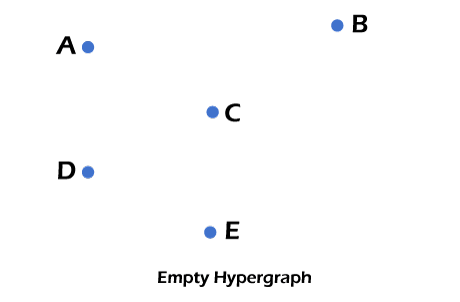
d - Regular: In this hypergraph, every vertex will contain a degree of d. This statement means that it is contained in precisely d hyperedges. Example: In the below hypergraph, there are degree 2, which is contained by all the vertices (A, B, and C). That's why this hypergraph is 2 regular hypergraphs. 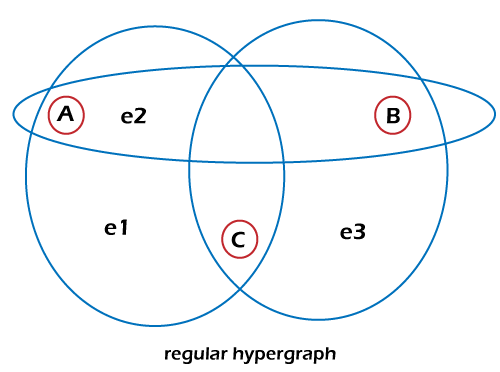
2- Colorable: The vertices of 2-colorable are divided into the two classes named P and Q. With the help of these classes, each hyperedge with a cardinality of a minimum 2 contains the minimum 1 vertex from each class. Non-Simple: The non-simple hypergraph will contain loops, which can be defined as hyperedges with a single vertex or repeated edges, which can be defined as two or more than two edges containing the same set of vertices. Example: In the following diagram, we can see that there are 2 loops named: e1 and e2. So this hypergraph is a non-simple hypergraph. 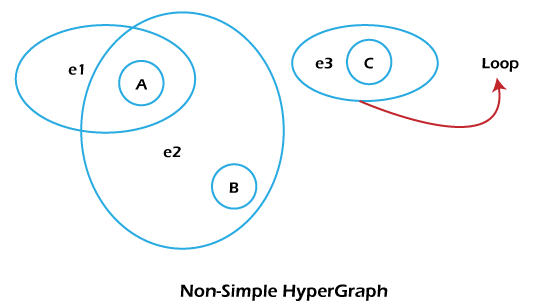
Simple: The simple hypergraph does not contain any loops or repeated edges. K uniform: In this, each hyperedge will be created with the help of exactly k vertices. Example: In the below hypergraph, we can see that there are 4 hyperedges: e1, e2, e3, and e4, and each hyperedge has 2 vertices. So we can say that this hypergraph is a 2 uniform hypergraph. 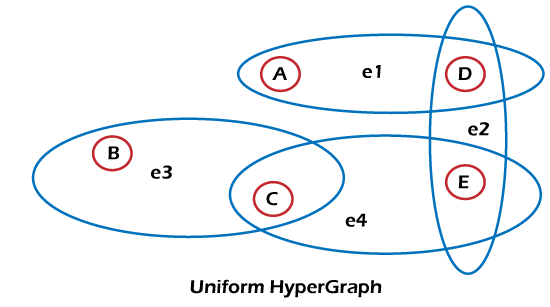
K partite: In this hypergraph, each hyperedge is comprised into one vertex of each type, and the vertices in this hypergraph are divided into the k parts. Example: In the below hypergraph, we can see that there are 3 parts in which vertices are divided, i.e., (A, D), (B, E), and (D, F). In this image, there is only 1 vertex contained by each hyperedge for each partition. 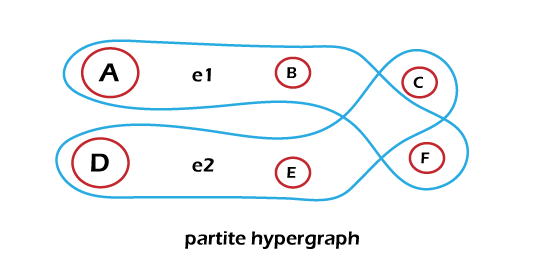
Next TopicHashing Function in Discrete mathematics
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










