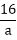Subgroup:If a non-void subset H of a group G is itself a group under the operation of G, we say H is a subgroup of G. Theorem: - A subset H of a group G is a subgroup of G if:
Cyclic Subgroup:-A Subgroup K of a group G is said to be cyclic subgroup if there exists an element x∈ G such that every element of K can be written in the form xn for some n ∈Z. The element x is called generator of K and we write K= <x> Cyclic Group:-In the case when G= Example: The group G= {1, -1, i,-i} under usual multiplication is a finite cyclic group with i as generator, since i1=i,i2=-1,i3=-i and i4=1 Abelian Group:Let us consider an algebraic system (G,*), where * is a binary operation on G. Then the system (G,*) is said to be an abelian group if it satisfies all the properties of the group plus a additional following property: (1) The operation * is commutative i.e., Example: Consider an algebraic system (G, *), where G is the set of all non-zero real numbers and * is a binary operation defined by 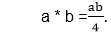
Show that (G, *) is an abelian group. Solution: Closure Property: The set G is closed under the operation *, since a * b = Associative Property: The operation * is associative. Let a,b,c∈G, then we have 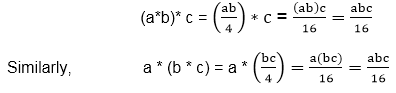
Identity: To find the identity element, let us assume that e is a +ve real number. Then e * a = a, where a ∈G. 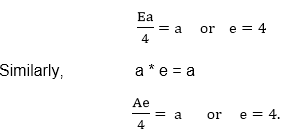
Thus, the identity element in G is 4. Inverse: let us assume that a ∈G. If a-1∈Q, is an inverse of a, then a * a-1=4 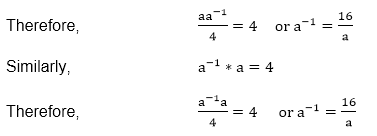
Thus, the inverse of element a in G is Commutative: The operation * on G is commutative. 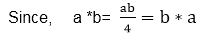
Thus, the algebraic system (G, *) is closed, associative, identity element, inverse and commutative. Hence, the system (G, *) is an abelian group. Product of Groups:Theorem: Prove that if (G1,*1)and (G2,*2) are groups, then G = G1 x G2 i.e., (G, *) is a group with operation defined by (a1,b1)*( a2,b2 )=(a1,*1,a2, b1 *2 b2). Proof: To prove that G1 x G2 is a group, we have to show that G1 x G2 has the associativity operator, has an identity and also exists inverse of every element. Associativity. Let a, b, c ∈ G1 x G2,then So, a * (b * c) = (a1,a2 )*((b1,b2)*(c1,c2)) Identity: Let e1 and e2 are identities for G1 and G2 respectively. Then, the identity for G1 x G2 is e=(e1,e2 ).Assume same a ∈ G1 x G2 Then, a * e = (a1,a2)*( e1,e2) Similarly, we have e * a = a. Inverse: To determine the inverse of an element in G1 x G2, we will determine it component wise i.e., Now to verify that this is the exact inverse, we will compute a * a-1 and a-1*a. Now, a * a-1=(a1,a2 )*(a1-1,a2-1 ) Similarly, we have a-1*a=e. Thus, (G1 x G2,*) is a group. In general, if G1,G2,....Gn are groups, then G = G1 x G2 x.....x Gn is also a group. Cosets:Let H be a subgroup of a group G. A left coset of H in G is a subset of G whose elements may be expressed as xH={ xh | h ∈ H } for any x∈ G. The element x is called a representation of the coset. Similarly, a right coset of H in G is a subset that may be expressed as Hx= {hx | h ∈H } , for any x∈G. Thus complexes xH and Hx are called respectively a left coset and a right coset. If the group operation is additive (+) then a left coset is denoted as x + H={x+h | h ∈H} and a right coset is denoted by H + x = {h+x | h ∈ H}
Next TopicNormal Subgroup
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





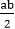 is a real number. Hence, it belongs to G.
is a real number. Hence, it belongs to G.