Types of Graphs:1. Null Graph: A null graph is defined as a graph which consists only the isolated vertices. Example: The graph shown in fig is a null graph, and the vertices are isolated vertices. 
2. Undirected Graphs: An Undirected graph G consists of a set of vertices, V and a set of edge E. The edge set contains the unordered pair of vertices. If (u, v)∈E then we say u and v are connected by an edge where u and v are vertices in the set V. Example: Let V = {1, 2, 3, 4} and E = {(1, 2), (1, 4), (3, 4), (2, 3)}.Draw the graph. Solution: The graph can be drawn in several ways. Two of which are as follows: 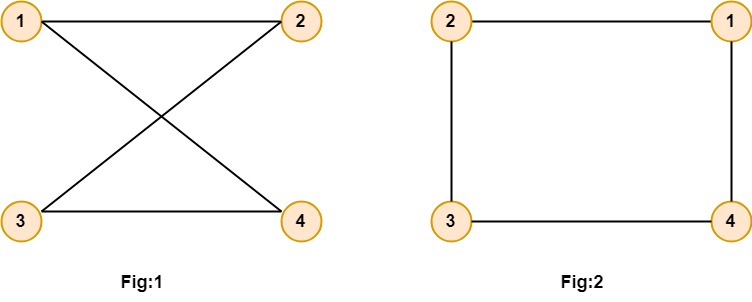
3. Multigraph: If in a graph multiple edges between the same set of vertices are allowed, it is known as Multigraph. In other words, it is a graph having at least one loop or multiple edges. 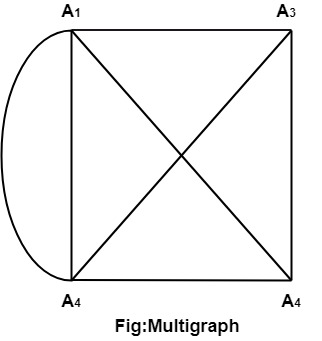
4. Directed Graphs: A directed graph or digraph G is defined as an unordered pair (V, E), where V is the set of points called vertices and E is the set of edges. Each edge in the graph G is assigned a direction and is identified with an ordered pair (u, v), where u is the initial vertex, and v is the end vertex. Example: Consider the graph G = (V, E) as shown in fig. Determine the vertex set and edge set of graph G. 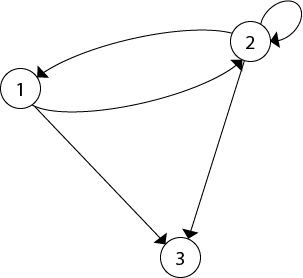
Solution: The vertex and edge set of graph G =(V, E) is as follow G={{1,2,3},{(1,2),(2,1),(2,2),(2,3),(1,3)}}.5. Undirected Complete Graph: An undirected complete graph G=(V,E) of n vertices is a graph in which each vertex is connected to every other vertex i.e., and edge exist between every pair of distinct vertices. It is denoted by Kn.A complete graph with n vertices will have Example: Draw Undirected Complete Graphs k4and k6. Solution: The undirected complete graph of k4 is shown in fig1 and that of k6is shown in fig2. 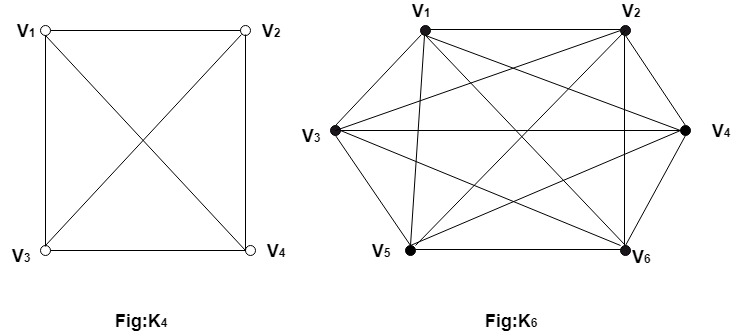
6. Connected and Disconnected Graph: Connected Graph: A graph is called connected if there is a path from any vertex u to v or vice-versa. Disconnected Graph: A graph is called disconnected if there is no path between any two of its vertices. Example: Consider the graph shown in fig. Determine whether the graphs are (a)Disconnected Graph (b)Connected Graph. Also, write their connected components. 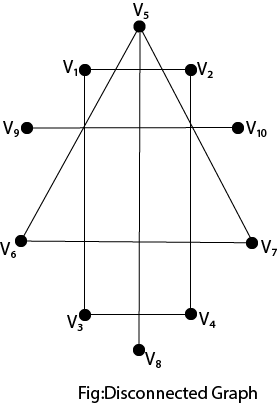
Solution: (i) The graph is shown in fig is a Disconnected Graph, and its connected components are {V1,V2,V3,V4},{V5,V6,V7,V8} and {V9,V10}. (ii) The graph shown in fig is a Disconnected Graph and its connected components are {V1,V2},{V3,V4},{V5,V6},{V7,V8},{V9,V10}and {V11,V12}. 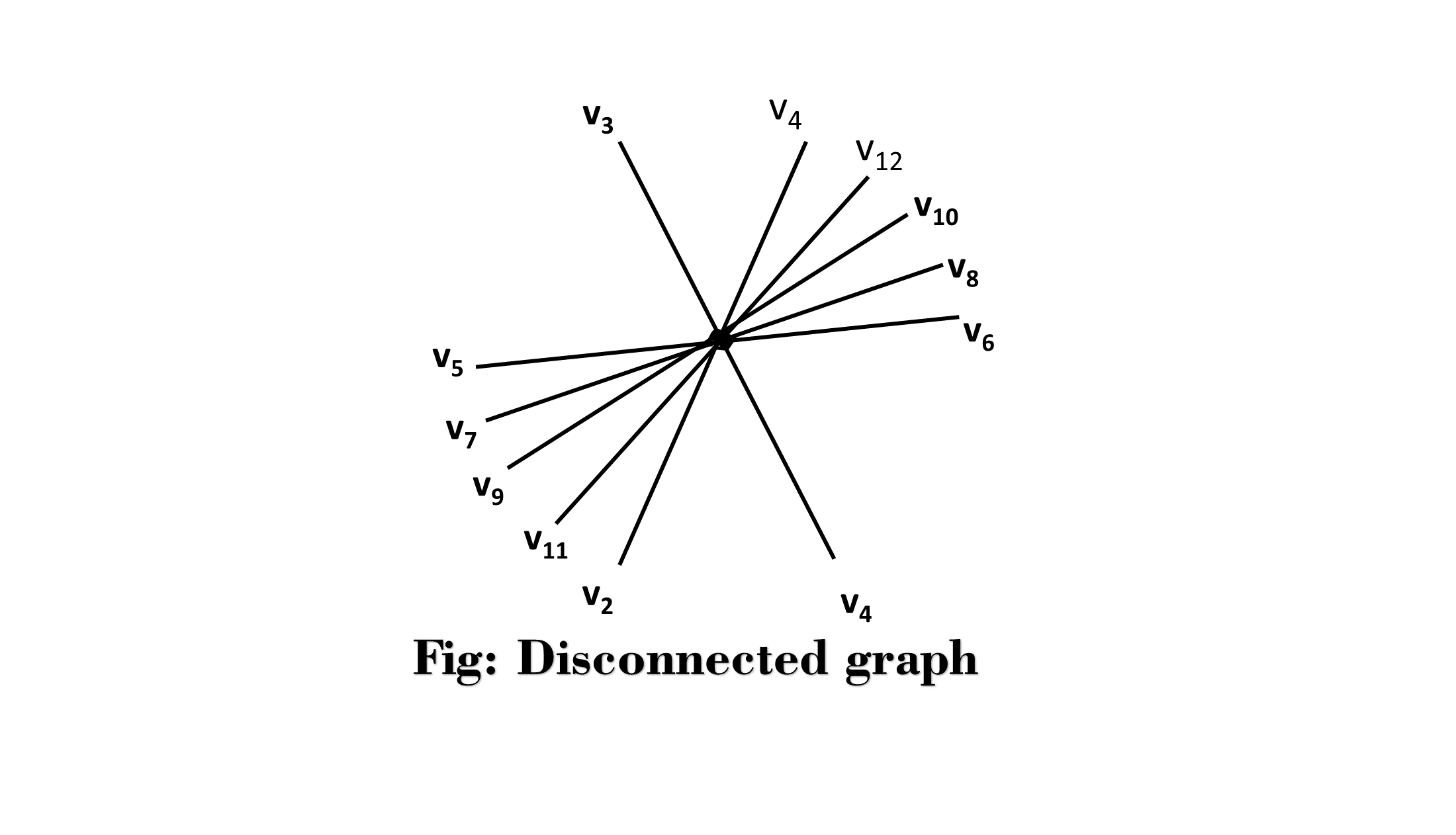
(iii) The graph shown in fig is a connected graph. 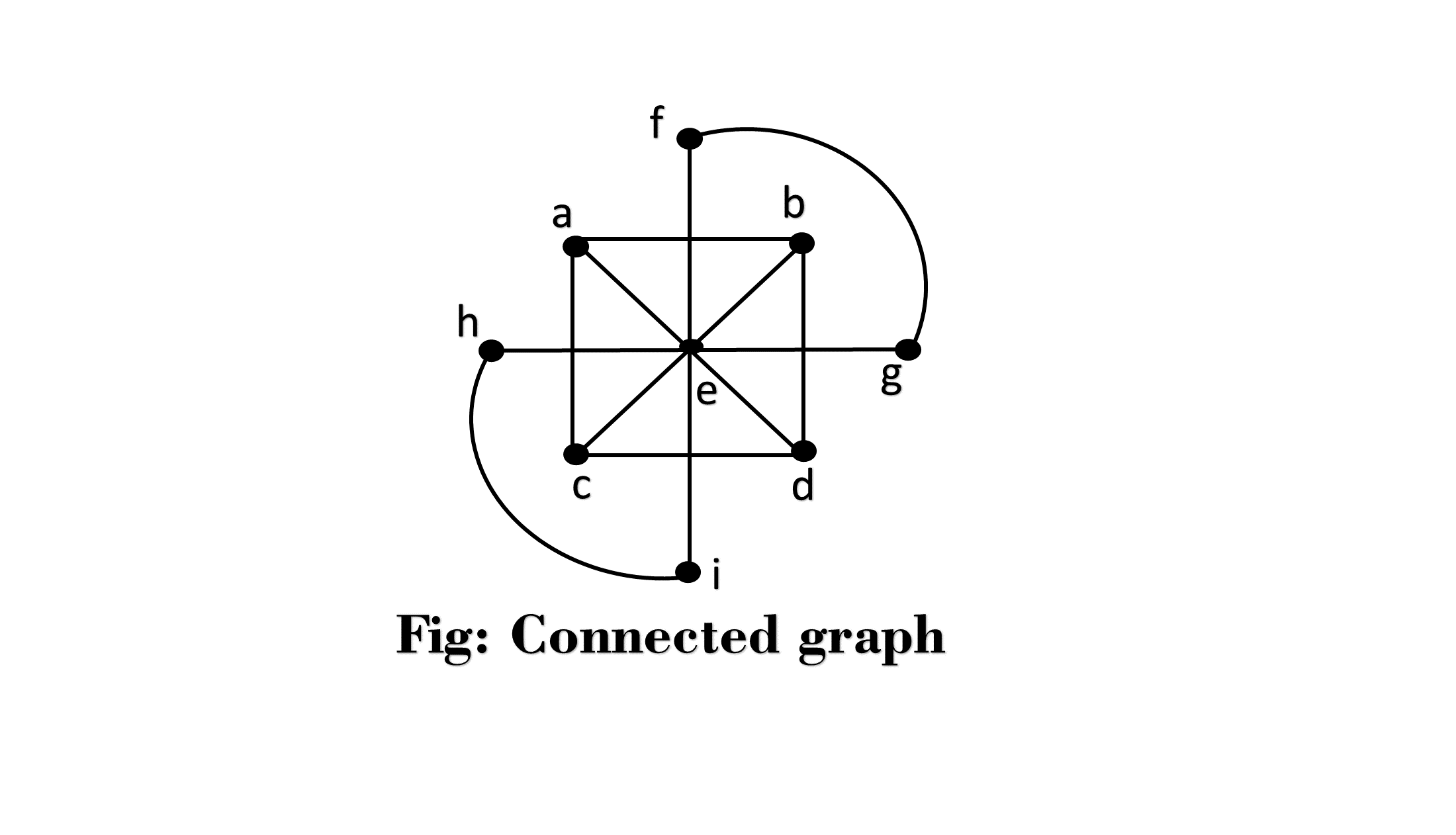
7. Connected Component: A subgraph of graph G is called the connected component of G, if it is not contained in any bigger subgraph of G, which is connected. It is defined by listing its vertices. Example: Consider the graph shown in fig. Determine its connected components. 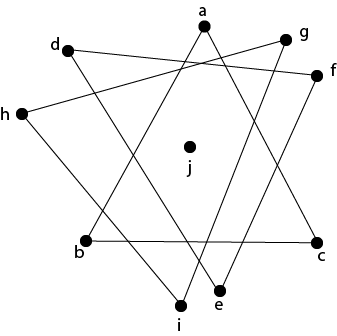
Solution: The connected components of this graph is {a, b, c}, {d, e, f}, {g, h ,i} and {j}. 8. Directed Complete Graph: A directed complete graph G = (V, E) on n vertices is a graph in which each vertex is connected to every other vertex by an arrow. It is denoted by Kn. Example: Draw directed complete graphs K3 and K5. Solution: Place the number of vertices at the appropriate place and then draw an arrow from each vertex to every other vertex as shown in fig: 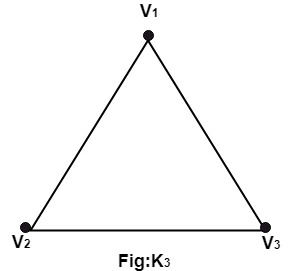 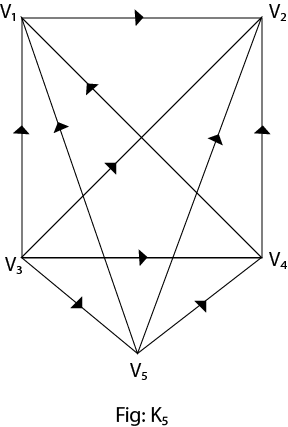
9. Complementary Graph: The complement of a graph G is defined to be a graph which has the same number of vertices as in graph G and has two vertices connected if and only they are not related in the graph. Example: Consider the graph G shown in fig. Find the complement of this graph. 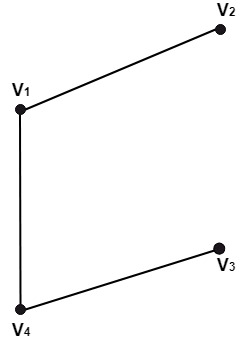
Solution: The complement of the above graph is shown in Fig: 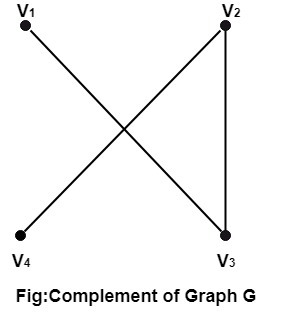
10. Labeled Graphs: A graph G=(V, E) is called a labeled graph if its edges are labeled with some name or data. So, we can write these labels in place of an ordered pair in its edges set. Example: The graph shown in fig is labeled graphs. G= {{a, b, c, d}, {e1,e2,e3,e4}} 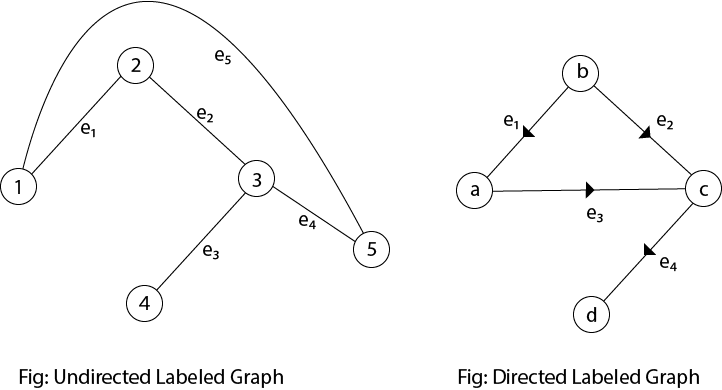
11.Weighted Graphs: A graph G=(V, E) is called a weighted graph if each edge of graph G is assigned a positive number w called the weight of the edge e. Example: The graph shown in fig is a Weighted Graph. 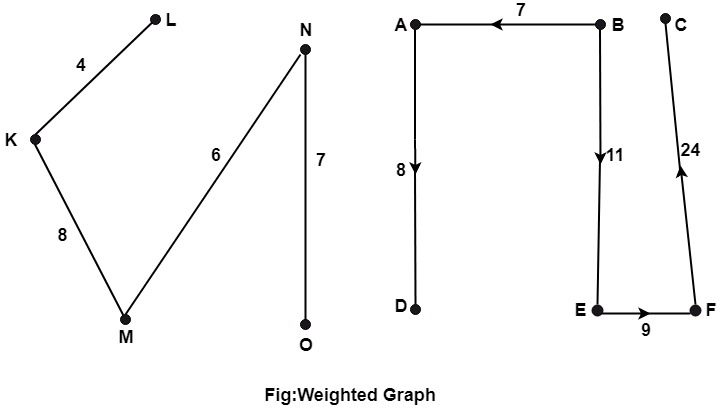
Next TopicRepresentation of Graphs
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




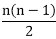 edges.
edges.




