Types of SetsSets can be classified into many categories. Some of which are finite, infinite, subset, universal, proper, power, singleton set, etc. 1. Finite Sets: A set is said to be finite if it contains exactly n distinct element where n is a non-negative integer. Here, n is said to be "cardinality of sets." The cardinality of sets is denoted by|A|, # A, card (A) or n (A). Example:
2. Infinite Sets: A set which is not finite is called as Infinite Sets. Countable Infinite: If there is one to one correspondence between the elements in set and element in N. A countably infinite set is also known as Denumerable. A set that is either finite or denumerable is known as countable. A set which is not countable is known as Uncountable. The set of a non-negative even integer is countable Infinite. Uncountable Infinite: A set which is not countable is called Uncountable Infinite Set or non-denumerable set or simply Uncountable. Example: Set R of all +ve real numbers less than 1 that can be represented by the decimal form 0. a1,a2,a3..... Where a1 is an integer such that 0 ≤ ai ≤ 9. 3. Subsets: If every element in a set A is also an element of a set B, then A is called a subset of B. It can be denoted as A ⊆ B. Here B is called Superset of A. Example: If A= {1, 2} and B= {4, 2, 1} the A is the subset of B or A ⊆ B. Properties of Subsets:
4. Proper Subset: If A is a subset of B and A ≠ B then A is said to be a proper subset of B. If A is a proper subset of B then B is not a subset of A, i.e., there is at least one element in B which is not in A. Example: (i) Let A = {2, 3, 4} A is a proper subset of B. (ii) The null ∅ is a proper subset of every set. 5. Improper Subset: If A is a subset of B and A = B, then A is said to be an improper subset of B. Example (i) A = {2, 3, 4}, B = {2, 3, 4} A is an improper subset of B. (ii) Every set is an improper subset of itself. 6. Universal Set: If all the sets under investigations are subsets of a fixed set U, then the set U is called Universal Set. Example: In the human population studies the universal set consists of all the people in the world. 7. Null Set or Empty Set: A set having no elements is called a Null set or void set. It is denoted by∅. 8. Singleton Set: It contains only one element. It is denoted by {s}. Example: S= {x|x∈N, 7<x<9} = {8} 9. Equal Sets: Two sets A and B are said to be equal and written as A = B if both have the same elements. Therefore, every element which belongs to A is also an element of the set B and every element which belongs to the set B is also an element of the set A. If there is some element in set A that does not belong to set B or vice versa then A ≠ B, i.e., A is not equal to B. 10. Equivalent Sets: If the cardinalities of two sets are equal, they are called equivalent sets. Example: If A= {1, 2, 6} and B= {16, 17, 22}, they are equivalent as cardinality of A is equal to the cardinality of B. i.e. |A|=|B|=3 11. Disjoint Sets: Two sets A and B are said to be disjoint if no element of A is in B and no element of B is in A. Example: R = {a, b, c} R and S are disjoint sets. 12. Power Sets: The power of any given set A is the set of all subsets of A and is denoted by P (A). If A has n elements, then P (A) has 2n elements. Example: A = {1, 2, 3} Partitions of a Set:Let S be a nonempty set. A partition of S is a subdivision of S into nonoverlapping, nonempty subsets. Speceficially, a partition of S is a collection {Ai} of nonempty subsets of S such that:
Aj≠ Ak Then Aj ∩ Ak= ∅ The subsets in a partition are called cells. Fig: Venn diagram of a partition of the rectangular set S of points into five cells,A1,A2,A3,A4,A5 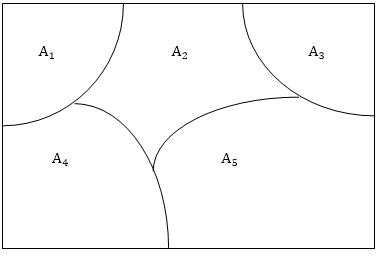
Venn Diagrams:Venn diagram is a pictorial representation of sets in which an enclosed area in the plane represents sets. Examples: 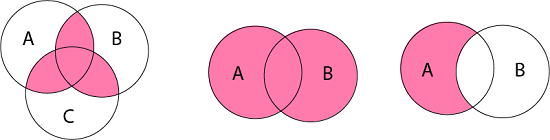
Next TopicSets Operations
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









