Compositions of Functions

Consider functions, f: A → B and g: B → C. The composition of f with g is a function from A into C defined by (gof) (x) = g [f(x)] and is defined by gof.

      To find the composition of f and g, first find the image of x under f and then find the image of f (x) under g.

Example1:

Consider the function f = {(1, a), (2, a), (3, b)} and g = {(a, 5), (b, 7)} as in figure. Find the composition of gof.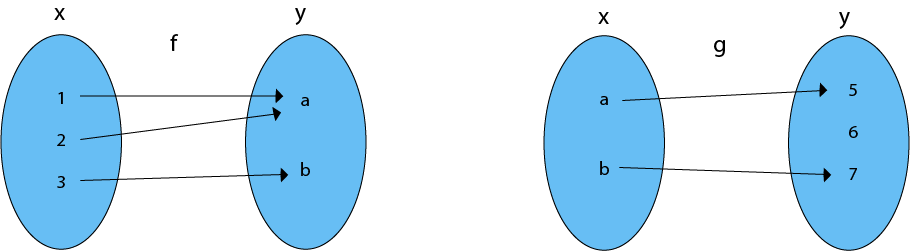

Solution: The composition function gof is shown in fig: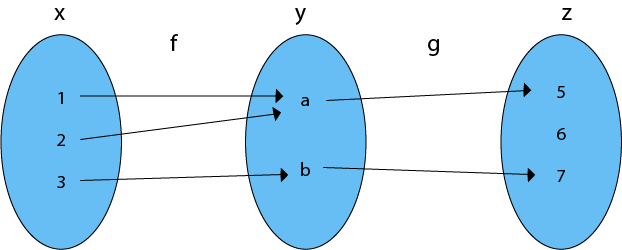

(gof) (1) = g [f (1)] = g (a) = 5, (gof) (2) = g [f (2)] = g (a) = 5
(gof) (3) = g [f (3)] = g (b) = 7.

Example2: Consider f, g and h, all functions on the integers, by f (n) =n², g (n) = n + 1 and h (n) = n - 1.

Determine (i) hofog       (ii) gofoh       (iii) fogoh.

Solution:

(i) hofog (n) = n + 1,
    hofog (n + 1) = (n+1)2 
h [(n+1)2 ] = (n+1)2 - 1 = n2 + 1 + 2n - 1 = n2 + 2n.

(ii) gofoh (n) = n - 1, gof (n - 1) = (n-1)2 
     g [(n-1)2 ] = (n-1)2 + 1 = n2 + 1 - 2n + 1 = n2 - 2n + 2.
	 
(iii) fogoh (n) = n - 1
      fog (n - 1) = (n - 1) + 1
      f (n) = n2.

Note:

• If f and g are one-to-one, then the function (gof) (gof) is also one-to-one.
• If f and g are onto then the function (gof) (gof) is also onto.
• Composition consistently holds associative property but does not hold commutative property.