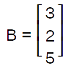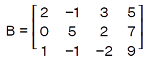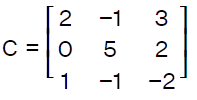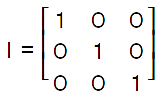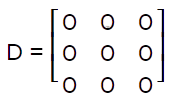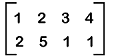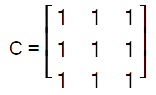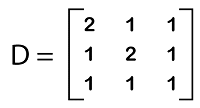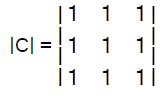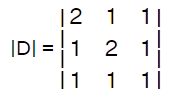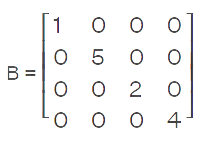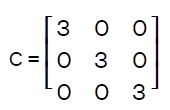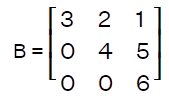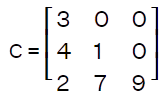Type of matrices in Discrete mathematics

We will discuss little bit about matrices because we are going to discuss about the types of matrices in this section. A matrix is used to contain the rectangular array of numbers, and all these numbers, expressions, or symbols will be arranged in the form of rows and columns. With the help of a number of rows and columns, we can determine the order of matrix. If there is more than one matrix, then it will be known as the matrices. In any matrix, the entries are known as the numbers, and each number is an element. We can refer to the size of the matrix as m by n, and we can write it as m∗n. Here n is used to indicate the number of rows, and m is used to indicate the number of columns.

Discrete mathematics contains many types of matrices. Based on the order, element, and certain set of conditions of the matrices, we can differentiate all these types of matrices. The word "matrices" is used to indicate the plural form of a matrix. We will use the term in this section to indicate more than one matrix. In this section, we are going to learn about different types of matrices, their definitions, and many examples.

What are Types of matrices

Here we will show some important types of matrices which are used in the field of discrete mathematics, science, and engineering. The various types of matrices in discrete mathematics are described as follows:

• Row and column matrix
• Rectangular matrix and square matrix
• Horizontal matrix and vertical matrix
• Singleton matrix
• Identity matrix
• Zero matrix
• Diagonal matrix
• Singular matrix and on singular matrix
• Hermitian matrix and Skew Hermitian matrix
• Upper and lower triangular matrix
• Symmetric matrix and Skew symmetric matrix
• Orthogonal matrix

With the help of above types of matrices, we can organize data on the basis of age, month, person, group, company, and many more things. By using this information, we can make decisions and solve various kinds of math problems.

Identifying types of matrices

There are various sizes in which the matrices can be represented, but usually, the shape of the matrices remains the same. The size of the matrix will be known as its order. We can calculate it with the help of counting the total number of rows and columns in a matrix. The following image will show the procedure for finding the dimension of a given matrix.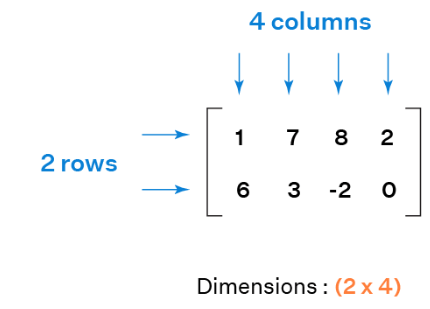

Now we will learn about the most commonly used matrices and how we can find them on the basis of their dimension.

Row and column matrix

A matrix will be known as a row matrix if there is any number of columns, but it must contain only 1 row. Suppose there is a matrix A = [aij]_m∗n, then this matrix will be a row matrix if m = 1. So we can represent the row matrix as A = [aij]_1∗n. Hence the order of row matrix will be 1∗n.

Similarly, a matrix will be known as a column matrix if there is any number of rows, but it must contain only 1 column. Suppose there is a matrix A = [aij]_m∗n, then this matrix will be a column matrix if n = 1. So we can represent the column matrix as A = [aij]_m∗1. Hence the order of column matrix will be m∗1. The example of calculating the row and column matrix is described as follows:

Row matrix	Column matrix
A = [1 0 2 4]
Matrix A is known as the row matrix because it has only one row.	Matrix B is known as the column matrix because it contains only one column.

Rectangular and Square matrix

A matrix will be known as a rectangular matrix if it does not contain an equal number of rows and columns. It can be indicated with the help of symbol B_m∗n.

Similarly, a matrix will be known as a square matrix if it contains an equal number of rows and columns. It can be indicated with the help of symbol B_n∗n. The example of calculating the rectangular matrix and square matrix is described as follows:

Rectangular matrix	Square matrix
Matrix B is known as the rectangular matrix because it contains 3 rows and 4 columns.	Matrix C is known as the square matrix because it has 3 rows and 3 columns.

Identify and Zero matrices

A matrix will be known as the identity matrix if the main diagonal elements of the square matrix are equal to 1 and all the remaining entries or elements of this matrix are equal to 0. The identity matrix can be indicated with the help of symbol I.

Note:

• If there are identity matrices, then they must be scalar matrices.
• If there are scalar matrices, then they must be diagonal matrices.
• If there are diagonal matrices, then they must be square matrices.
• It is not possible to do the converse of all these statements.

A matrix will be known as a zero matrix if all the elements of this matrix are equal to zero. The zero matrix is indicated with the help of symbol 0. The example of calculating the identity matrix and zero matrix is described as follows:

Identity matrix	Zero matrix
Matrix I is known as the identity matrix because the diagonal elements of this matrix are 1 and all the remaining elements are 0.	Matrix D is known as the zero matrix because all the elements of this matrix are 0.

Equal matrix

The matrices will be known as equal matrices if their elements are equal to each other. There are conditions in case of matrix equality, which are described as follows:

Suppose there are two matrices, A and B. These matrices will be equal if and only if the order and the corresponding elements of these matrices are similar to each other. Suppose A = [aij]_m∗n and B = [bij]_m∗n. These matrices will be equal if it contains the following:

• If m = r. It shows that the number of rows in matrix A is equal to the number of rows in matrix B.
• If n = s. It shows that the number of columns in matrix A is equal to the number of columns in matrix B.
• If there is a case where aij = bij for i = 1, 2, 3, ...., m and j = 1, 2, 3, ...., n. It indicates that the corresponding elements of both are equal.

For example: Suppose there are two matrices, which are described as follows: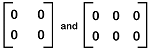

In the above image, the first matrix is in the order 2∗2, and the second matrix is in the order 2∗3. So both the matrices do not contain the same number of orders. That's why these matrices are not equal.

Suppose we have two more matrices, which are described as follows: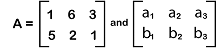

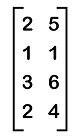
In this image, both the matrices contain the order 2∗3. So these matrices will be equal to each other. So we can assign the following values to the matrix:

a1 = 1, a2 = 6, a3 = 3, b1 = 5, b2 = 2, b3 = 1.

Horizontal and Vertical matrix

A matrix will be known as the horizontal matrix if it contains an order m∗n where n>m. Here m is used to indicate the number of rows, and n is used to indicate the number of columns. So for a horizontal matrix, the number of columns must be greater than the number of rows.

Similarly, a matrix will be known as the vertical matrix if it contains an order m∗n where m>n. So for a vertical matrix, the number of rows must be greater than the number of columns.

The example of calculating the horizontal matrix is described as follows:

Horizontal matrix	Vertical matrix
This matrix is known as the horizontal matrix because it contains 2 rows and 4 columns. That means the number of columns is greater than the number of rows.	Matrix C is known as the vertical matrix because it contains 4 rows and 2 columns. That means the number of rows is greater than the number of columns.

Other types of matrices

There are a lot of other matrices that can be used in discrete mathematics apart from the most commonly used matrix, which we have already explained. All these matrices are described as follows:

Singular and Non-singular matrix

A matrix will be known as a singular matrix if the determinant of the given square matrix is equal to 0.

A matrix will be known as a non-singular matrix if the determinant of the given square matrix is not equal to 0. With the help of determinant formula, we can determine the determinant of a matrix. The example of calculating the singular matrix and non-singular matrix is described as follows:

Singular matrix	Non-singular matrix
= 1∗ (1∗1 - 1∗1) -1∗(1∗1 - 1∗1) +1∗(1∗1 - 1∗1) = 1∗(1-1) -1∗(1-1) +1∗(1-1) = 1∗(0) -1∗(0) +1∗(0) = 0 + 0 + 0 = 0	= 2∗ (2∗1 - 1∗1) -1∗(1∗1 - 1∗1) +1∗(1∗1 - 2∗1) = 2∗(2-1) -1∗(1-1) +1∗(1-2) = 2∗(1) -1∗(0) +1∗(-1) = 2 - 0 - 1 = 1
Matrix C is known as the singular matrix because |C| = 0.	Matrix D is known as the non-singular matrix because |D| ? 0.

Diagonal matrix and Scalar matrix

A matrix will be known as the diagonal matrix if all elements of the square matrix are 0 except for the diagonal elements of the matrix. Suppose there is a square matrix A = [aij]. This matrix will be a diagonal matrix if aij = 0 when i ? j. So in case of a diagonal matrix, the diagonal elements contain the non-zero elements, and all non-diagonal elements contain zero. The diagonal matrix is used to contain two important points, which are described as follows:

1. The diagonal matrix must be a square matrix.
2. With the help of form aij, we can characterize the diagonal elements where i = j. It is used to show that a matrix can contain only one diagonal.

Some examples of diagonal matrices are described as follows: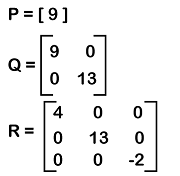

In this image, there are three diagonal matrices, P, Q, and R, which contain the order 1∗1, 2∗2, and 3∗3, respectively.

A scalar matrix is a different kind of diagonal matrix. A matrix will be known as a scalar matrix if all the diagonal elements of the given square matrix are similar to each other and all the other elements except diagonal elements are 0. There is a special type of square diagonal matrix, which is called a scalar matrix. The example of calculating the diagonal matrix and scalar matrix is described as follows:

Diagonal matrix	Scalar matrix
Matrix B is known as the diagonal matrix because all the elements of this matrix are 0 except for the diagonal matrix.	Matrix C is known as the scalar matrix because the diagonal elements of the above square matrix are similar to each other, and all the other elements are 0.

Upper and Lower triangular matrix

A matrix will be known as the upper triangular matrix if there is a square matrix in which all the elements which are below diagonal elements are equal to 0.

Similarly, a matrix will be known as the lower triangular matrix if there is a square matrix in which all the elements which are above diagonal elements are equal to 0. The example of calculating both types of triangular matrices are described as follows:

Upper triangular matrix	Lower triangular matrix
Matrix B is known as the upper triangular matrix because all the elements, which are shown under the main diagonal are equal to 0.	Matrix B is known as the lower triangular matrix because all the elements which are shown above the main diagonal are equal to 0.

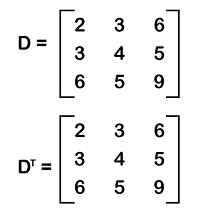
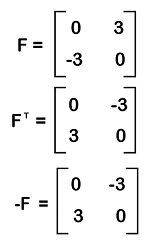
Symmetric and Skew symmetric matrix

If there is a square matrix D which contains the size n∗n, then this type of matrix will be known as the symmetric matrix if D^T = D. Here, T is used to indicate the transpose of a matrix.

If there is a square matrix F which contains the size n∗n, then this type of matrix will be known as the skew-symmetric matrix if F^T = -F. The example of calculating the symmetric matrix and skew-symmetric matrix is described as follows:

Symmetric matrix	Skew symmetric matrix
Matrix D is known as the symmetric matrix because DT and D both are equal to each other.	Matrix F is known as the skew-symmetric matrix because FT and -F both are equal to each other.

Note:

• If there is a square matrix A, in this case, there will be a symmetric matrix A + A^T and a skew-symmetric matrix A - A^T.
• We can uniquely express the square matrix in the form of addition of a symmetric matrix and a skew-symmetric matrix, which is described as follows:
  A = ½(A + A^T) + ½(A - A^T) = ½(B + C)
• Here, B is used to indicate the symmetric matrix, and C is used to indicate the skew-symmetric matrix.
• If there are two symmetric matrices, A and B, in this case, AB will be symmetric AB = BA. That means A and B are commutative.
• If there is a matrix A which is a symmetric or skew-symmetric matrix, in this case, the matrix B^TAB will be symmetric or non-symmetric in correspondence.
• In the symmetric matrix, all positive integral powers will always be symmetric.
• If there is a skew-symmetric matrix that contains positive odd integral power, then it will always be skew-symmetric. If there is a skew-symmetric matrix that contains positive even integral power, then it will always be symmetric.

Hermitian and Skew Hermitian matrices

The hermitian and skew-hermitian matrices are used to have a very small difference, which is described as follows:

A given matrix will be known as the hermitian matrix if this matrix and the transpose of its conjugate matrix are similar to each other. The example of calculating the hermitian matrix is described as follows: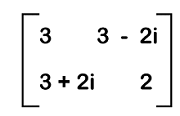

A given matrix will be known as the skew hermitian matrix if this matrix and the negation of its conjugate matrix are similar to each other. The example of calculating the skew hermitian matrix is described as follows: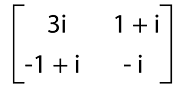

Boolean matrix

If all the elements of a given matrix are either 0s or 1s, only then the given matrix will be known as the Boolean matrix. The example of calculating the Boolean matrix with the help of matrix B is described as follows: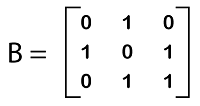

Stochastic matrices

If all the entries of the given matrix represent probability, only then the given matrix will be known as the stochastic matrix. A stochastic matrix can be of two types: left stochastic matrix and right stochastic matrix. If the entries of the given square matrix C are non-negative and the addition of entries of each column is equal to 1, only then the given square matrix will be left stochastic matrix. Similarly, if the entries of the given square matrix are non-negative and the addition of entries of each row is equal to 1, only then the given square matrix will be a right stochastic matrix. The example of calculating the left stochastic matrix C is described as follows:

Orthogonal matrix

If there is a square matrix B that contains the relation B∗B^T = I, then this type of matrix will be known as the orthogonal matrix. Here B^T is used to indicate the transpose of matrix B, and I is used to indicate the identity matrix. The example of calculating the orthogonal matrix is described as follows: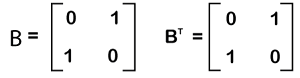

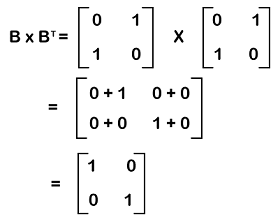
Here matrix B is known as the orthogonal matrix because B∗B^T = I.

Singleton matrix

A matrix will be known as a singleton matrix if it contains only one element in the given matrix. Suppose there is a matrix A = [ai∗j]_m∗n. So this matrix will be a singleton matrix if it m = n = 1. The example of a singleton matrix is described as follows:

[], [4], [6], [7], [a], etc

Special matrix

We have learned various types of matrices, but there are various special kinds of matrices, which are described as follows:

Idempotent matrix

If there is a square matrix A which contain the relation Aⁿ = A for every n ≤ 2, then this type of matrix will be known as the idempotent matrix. For example: A² = A, A³ = A, and many more. By checking the condition A² = A, we can determine whether the square matrix is idempotent or not.

Nilpotent matrix

If there is a square matrix A that contains the relation A^k = 0 for some k ≤ n, then this type of matrix will be known as the nilpotent matrix. For example: Suppose there is a matrix A where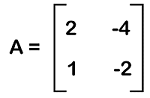

This matrix is a nilpotent matrix because A² = 0. Here 0 is used to indicate the null matrix of order 2.

Involutory matrix

If there is a square matrix A that contains the relation A^-1 = A, then this type of matrix will be known as the involutory matrix. For example: If there is an identity matrix, then it will definitely be an involutory matrix because it is equal to its inverse.

Important points

• A matrix will be known as the row matrix if there can be any number of columns, but it must contain only 1 row.
• A matrix will be known as the column matrix if there can be any number of rows, but it must contain only 1 column.
• A matrix will be known as a constant matrix if and only if all the elements of a matrix are constant for any given dimension or order of the matrix.