Operations on SetsThe basic set operations are: 1. Union of Sets: Union of Sets A and B is defined to be the set of all those elements which belong to A or B or both and is denoted by A∪B. Example: Let A = {1, 2, 3}, B= {3, 4, 5, 6} 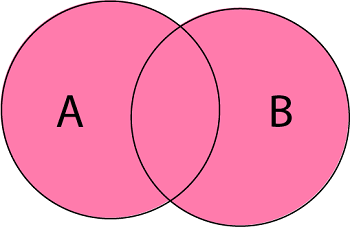 2. Intersection of Sets: Intersection of two sets A and B is the set of all those elements which belong to both A and B and is denoted by A ∩ B. Example: Let A = {11, 12, 13}, B = {13, 14, 15} 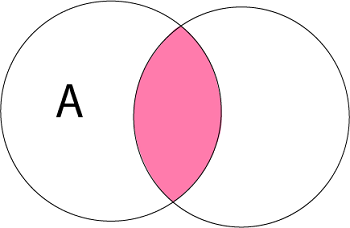 3. Difference of Sets: The difference of two sets A and B is a set of all those elements which belongs to A but do not belong to B and is denoted by A - B. Example: Let A = {1, 2, 3, 4} and B = {3, 4, 5, 6} then A - B = {3, 4} and B - A = {5, 6} 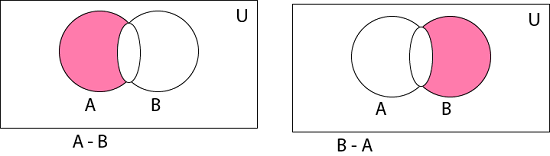 4. Complement of a Set: The Complement of a Set A is a set of all those elements of the universal set which do not belong to A and is denoted by Ac.
Ac = U - A = {x: x ∈ U and x ∉ A} = {x: x ∉ A}
Example: Let U is the set of all natural numbers. 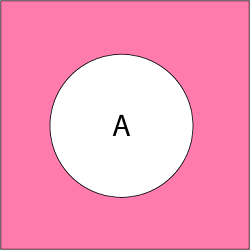 5. Symmetric Difference of Sets: The symmetric difference of two sets A and B is the set containing all the elements that are in A or B but not in both and is denoted by A ⨁ B i.e. Example: Let A = {a, b, c, d} 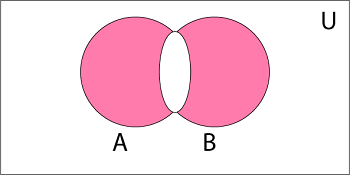
Next TopicAlgebra of Sets
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










