Dijkstra's Algorithm:

This algorithm maintains a set of vertices whose shortest paths from source is already known. The graph is represented by its cost adjacency matrix, where cost is the weight of the edge. In the cost adjacency matrix of the graph, all the diagonal values are zero. If there is no path from source vertex V_s to any other vertex V_i then it is represented by +∞.In this algorithm, we have assumed all weights are positive.

1. Initially, there is no vertex in sets.
2. Include the source vertex V_s in S.Determine all the paths from V_s to all other vertices without going through any other vertex.
3. Now, include that vertex in S which is nearest to V_s and find the shortest paths to all the vertices through this vertex and update the values.
4. Repeat the step until n-1 vertices are not included in S if there are n vertices in the graph.

After completion of the process, we got the shortest paths to all the vertices from the source vertex.

Example: Find the shortest paths between K and L in the graph shown in fig using Dijkstra's Algorithm.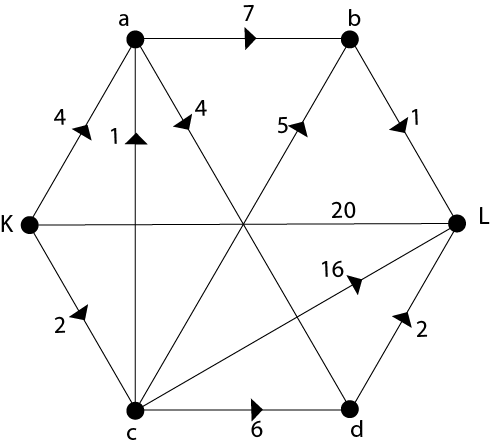

Solution:

Step1: Include the vertex K is S and determine all the direct paths from K to all other vertices without going through any other vertex.

Distance to all other vertices

Step2: Include the vertex in S which is nearest to K and determine shortest paths to all vertices through this vertex and update the values. The closest vertex is c.

Distance to all other vertices

Step3: The vertex which is 2^nd nearest to K is 9, included in S.

Distance to all other vertices

Step4: The vertex which is 3^rd nearest to K is b, included in S.

Distance to all other vertices

Step5: The vertex which is next nearest to K is d, is included in S.

Distance to all other vertices

Since, n-1 vertices included in S. Hence we have found the shortest distance from K to all other vertices. Thus, the shortest distance between K and L is 8 and the shortest path is K, c, b, L.