Probable error formula for discrete mathematics

Probable Error

The probable error can be described as a correlation coefficient. The value of the coefficients and their accuracy is fully dependent on the probable error. The image of probable error is described as follows: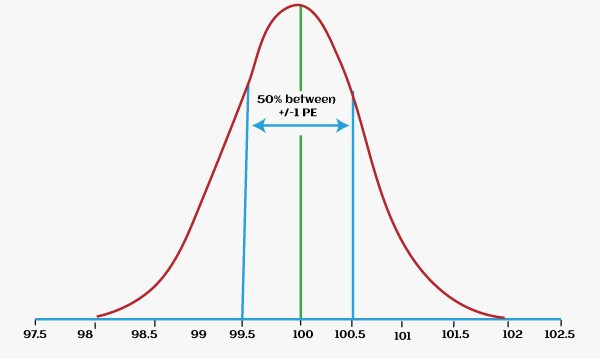

As we have described above, the probable error is a kind of correlation coefficient that is used to determine the accurate value of coefficients. It is also used to find out the reliability of coefficient.

The process or job of determining the bounds and limits of a correlation coefficient is very easy. With the help of samples, we can perform the calculation of correlation coefficient. These samples must be in pairs, which come from a very large population.

On the basis of the knowledge and sample relating to the correlation coefficient, the correlation coefficient for a population can be determined. With the help of probable error, we can very easily determine or obtain the correlation coefficient of any population. The formula to do this is described as follows:

Probable Error = 0.674 * (1- r2 / √N)

Here

r is used to indicate the correlation coefficient of 'n' pairs of observation for any random sample N is used to indicate the total number of observations

There are some facts related to this formula, which is described as follows:

• If the value of probable error is greater than the value of 'r', then the correlation between different values will occur hardly.
• If the value of error is around 6 times less than the value of 'r', only then there will be a certain value of correlation coefficient.
• The value of probable error always occurs in a certain boundary, i.e., -1 and +1(-1 ≤ r ≤ 1). With the help of following manner, we can express this boundary like this:

Probable Limit

When we add or subtract the value of probable error from the value of r, we will get the lower limit and upper limit. This is the place on which the correlation coefficient's value exactly lies:

Here,

rho is used to indicate the correlation coefficient of a population. It is also known as the limit of correlation of coefficient. Alongside,

Here SE is referred to as Standard Error of Correlation Coefficient. The formula to determine the standard error is described as follows:

Standard Error = (1 - r2) / √N

The standard error can be described as a standard deviation of any mean. The standard error is a type of sampling distribution of standard deviation. With the help of standard error, we can take any sort of estimate related to the standard deviation. Therefore, we are able to easily calculate and check the reliability of coefficient with the help of a probable error.

Advantages of Standard Error

• The standard error is used to determine and reduce the sample errors, and it is also measures the errors.
• The accuracy of estimate is determined with the help of a standard error of any mean.

Formula for Calculating Probable Error

To calculate the probable error, we have three formulas, and we can use anyone. The most common formula to calculate probable error is the first formula, which is described as follows:

P.E r product-moment = 0.6745 (1 - r2) / √N

If we want the probable error for rho, in this case, we will use the second formula. Here, we will calculate the value with the help of Spearman method. The formula for this is described as follows:

P.E. ρ = 0.6745(1 - ρ2) / √N {1 + 1.086ρ2 + 0.13ρ4 + .002ρ6}

If we want the Pearson coefficient 'r', in this case, we will use the third formula. With the help of transmutation formula and p, we can calculate the Pearson coefficient. Here r = 2 sin (πρ / 6). The formula for this is described as follows:

E r found from ρ= 0.7063 (1 - r2)√N { 1 + 1.042r2 + 0.008r4 + .002r6 }

Note: If the provided population is normal, only after that the above formulas, which we are using to find out probable error, will be valid.

Conditions to find Probable Error

There are some conditions that need to be satisfied to find the probable error. These conditions are described as follows:

1. There must be a bell-shaped curve of the given data. This statement describes that the data will provide us a normal frequency curve.
2. To measure the statistics from a sample, we will take the probable error.
3. There is an unbiased manner that must be followed to take off the sample items. The values of these items must be independent of each other.

Example 1: We have a 0.8 correlation coefficient and 25 pairs of samples. Now we have to find the probable error in this example.

Solution: We will calculate the outcome of this example with the help of using the most common method. Here, n = 25 and r = 0.8. Now we will use the first formula to do this, which is described as follows:

P.E = 0.6745 (1 - r2) / √N

After putting the above values, we will get

Probable error = 0.674 * {(1 - (0.8)2) / √25} 
		= 0.674 * {(1 - 0.64) / 5}
		= 0.674 * (0.36 / 5)
		? 0.0486

So we can say that the probable error is: 0.0486.

Example 2: In this example, we have a 0.7 correlation coefficient and 64 pairs of samples. Now we have to determine the probable error of correlation coefficient. We have to also determine the limits for population correlation coefficient.

Solution: Here, we will calculate the outcome of this example with the help of using the most common method. Here, n = 64 and r = 0.7. Now we will use the first formula to do this, which is described as follows:

P.E = 0.6745 (1 - r2) / √N

After putting the above values, we will get

Probable error = 0.674 * {(1 - (0.7)2) / 64} 
		= 0.674 * 0.06375
		? 0.043

So we get a probable error of 0.043. Now we will use this PE and find out the limits of population of correlation coefficient. For this, we will use the following formula:

After putting the values, we will get the following:

So the probable limit is (0.743, 0.657)