Mathematical InductionThe process to establish the validity of an ordinary result involving natural numbers is the principle of mathematical induction. Working RuleLet n0 be a fixed integer. Suppose P (n) is a statement involving the natural number n and we wish to prove that P (n) is true for all n ≥n0. 1. Basic of Induction: P (n0) is true i.e. P (n) is true for n = n0. 2. Induction Step: Assume that the P (k) is true for n = k. Example 1: Prove the follo2wing by Mathematical Induction: 1 + 3 + 5 +.... + 2n - 1 = n2. Solution: let us assume that. P (n) = 1 + 3 + 5 +..... + 2n - 1 = n2. For n = 1, P (1) = 1 = 12 = 1 It is true for n = 1................ (i) Induction Step: For n = r,
P (r) = 1 + 3 + 5 +..... +2r-1 = r2 is true......................... (ii)
Adding 2r + 1 in both sides
P (r + 1) = 1 + 3 + 5 +..... +2r-1 + 2r +1
= r2 + (2r + 1) = r2 + 2r +1 = (r+1)2..................... (iii)
As P(r) is true. Hence P (r+1) is also true.
From (i), (ii) and (iii) we conclude that.
1 + 3 + 5 +..... + 2n - 1 =n2 is true for n = 1, 2, 3, 4, 5 ....Hence Proved.
Example 2: Solution: For n = 1, It is true for n = 1. Induction Step: For n = r,................... (i) Adding (r+1)2 on both sides, we get
As P (r) is true, hence P (r+1) is true. 12 + 22 + 32 +......+ n2= Example3: Show that for any integer n Solution:
Let P (n) = 11n+2+122n+1
For n = 1,
P (1) = 113+123=3059=133 x 23
So, 133 divide P (1).................. (i)
Induction Step: For n = r,
P (r) = 11r+2+122r+1=133 x s............ (ii)
Now, for n = r + 1,
P (r+1) = 11r+2+1+122(r)+3=11[133s-122r+1] + 144. 122r+1
= 11 x 133s + 122r+1.133=133[11s+122r+1]=133 x t........... (iii)
As (i), (ii), and (iii) all are true, hence P (n) is divisible by 133.
Next TopicBinary Relation
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





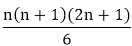
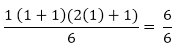 = 1
= 1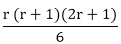 is true........... (ii)
is true........... (ii)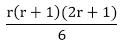 + (r+1)2
+ (r+1)2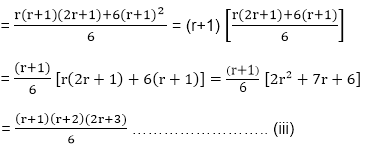
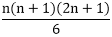 is true for n = 1, 2, 3, 4, 5 ..... Hence Proved.
is true for n = 1, 2, 3, 4, 5 ..... Hence Proved.




