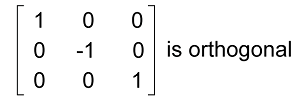Orthogonal matrix in Discrete mathematics

A matrix will be known as the orthogonal matrix if the transpose of the given matrix and its inverse matrix are similar to each other. Now we will learn about the transpose of a matrix. A matrix will be known as the transpose matrix if we interchange the elements of rows or columns of the original matrix. We already learned that if the original matrix and its transpose are similar to each other, then that matrix will be known as the symmetric matrix. But in the case of an orthogonal matrix, the inverse of the matrix and transpose of the matrix will be the same. In this section, we will learn about the orthogonal matrix, its definition, its determinant, its inverse, its properties, its examples, and many more.

What is an Orthogonal matrix

If there is a square matrix, then we can call it an orthogonal matrix if the transpose of this matrix and its inverse are similar to each other, i.e., A^T = A^-1. Here A^T is used to indicate the transpose of matrix A, and A^-1 is used to indicate the inverse of matrix A. There is one more definition of an orthogonal matrix on the basis of its definition, which is described as follows:

A^T = A^-1

Now we will multiply A on both sides of the above equation like this:

AA^T = AA^-1

As we have learned that AA^-1 = I, where I is used to indicate the identity matrix, which contains the same order as matrix A.

Thus AA^-1 = I.

In the same way, we can also prove that A^TA = I.

We will get the following equation from above two equations:

AA^T = A^TA = I.

Thus, an orthogonal matrix is used to contain two definitions which will be shown in the definition of an orthogonal matrix.

Definition of Orthogonal matrix

There are two definitions of an orthogonal matrix. According to the first definition, if the transpose of the matrix and the inverse of the matrix are similar to each other, then that matrix will be known as the orthogonal matrix. According to the second definition, if we get the identity matrix as the multiplication of given matrix and its transpose matrix, then the given matrix will be known as the orthogonal matrix.

Suppose there is a square matrix A, which contains the size n∗n. This matrix will be considered an orthogonal matrix if it contains the following conditions:

A^T = A^-1 (OR)

AA^T = A^TA = I

Note:

• It is necessary that all the orthogonal matrices will be invertible. The transpose holds back the determinant. This is because we can say that in the case of an orthogonal matrix, the determinant will always be +1 or -1.
• It is necessary that all the orthogonal matrices will be square matrices, but it is not compulsory that all the square matrices will be orthogonal.

Orthogonal matrix Example

In this example, we have a matrix A and its transpose matrix A^T. Here we have to multiply the given matrix and its transpose matrix. The elements of the given matrix are described as follows: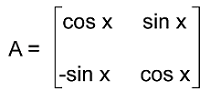

The transpose matrix is described as follows: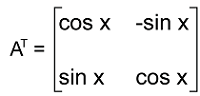

Now we will do the multiplication of both matrices in the following way: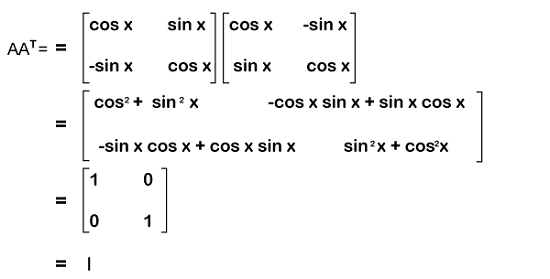

In the same way, we can also prove that AA^T = I. Therefore, matrix A is an example of the orthogonal matrix with an order 2∗2.

How to find Orthogonal matrix

There are some steps that should be followed to determine whether the matrix is an orthogonal matrix or not. For this, we will assume a square matrix A. These steps are described as follows:

Step 1: In this step, we will determine the determinant of the given matrix. The matrix A may be an orthogonal matrix if the determinant of this matrix is 1.

Step 2: In this step, we will determine the transpose of this matrix and the inverse of matrix.

Step 3: The matrix will be known as the orthogonal matrix if the multiplication of transpose of matrix A and inverse of matrix A will be an identity matrix, i.e., A^T ∗ A^-1 = I. Otherwise it will not be an orthogonal matrix. Here I is used to indicate the identity matrix.

Determinant of Orthogonal matrix

In case of the orthogonal matrix, if we calculate the determinant, then it will always be +1 or -1. Now we will prove it. For this, we will assume an orthogonal matrix A. With the help of its definition, we know that

AA^T = I

Now we will perform the determinant on both sides of the above equation and get the following:

det(AA^T) = det(I)

We have learned that we will get 1 if we determine the determinant of an identity matrix. Also, if there are two matrices, A and B, then det(AB) = detA ∗ detB. So

det(A) ∗ det(A^T) = 1

As we already know that det(A) = det(A^T). So

det(A) ∗ det(A) = 1

[det(A)]² = 1

det(A) = ±1

Inverse of Orthogonal matrix

With the help of definition of an orthogonal matrix, we know that any orthogonal matrix A, A^-1 = A^T. Now we will try to prove it with the help of this definition and also the other definition, i.e.,

AA^T = A^TA = I ...... (1)

If there are two matrices, A and B, then they will be inverse of each other if it satisfies the following condition:

AB = BA = I .... (2)

With the help of equations (1) and (2), we can see that B = A^T. Since B is the inverse of A, B = A^T is equivalent to A^-1 = A^T.

Thus it is proved that the inverse of an orthogonal matrix will be its transpose.

Properties of Orthogonal matrix

There are various properties of an orthogonal matrix on the basis of its definitions, and some of them are described as follows:

• The transpose and inverse of the orthogonal matrix are similar to each other, i.e., A^-1 = A^T.
• If we multiply the given matrix A and its transpose matrix, then we will get an identity matrix as a result, i.e., AA^T = A^TA = I.
• If the diagonal matrix is used to contain the elements 1 or -1, then it will always be orthogonal. For example,
  
• A^T is also orthogonal. If it contains the relation A^-1 = A^T, in this case, A^-1 will also be orthogonal.
• The eigenvectors will be orthogonal, and eigenvalues of A will be ±1.
• If there is an identity matrix (I), then it will be orthogonal, i.e., I.I = I.I = I.
• The orthogonal matrices will be symmetric in nature.
• The determinant of orthogonal matrix will be det(A) =±1. The determinant of this matrix is not 0. That's why an orthogonal matrix will always be non-singular.

Applications of Orthogonal matrix

There are various applications or uses in the orthogonal matrix, and some of them are described as follows:

• We can perform multi-channel signal processing with the help of an orthogonal matrix.
• We can perform multivariate time series analysis with the help of an orthogonal matrix.
• We can use this matrix in many algorithms in linear algebra.
• We can use this matrix in QR decomposition.

Important notes on Orthogonal matrix

There are some important points that we should know while learning the concept of an orthogonal matrix. These points are described as follows:

• The matrix will be an orthogonal matrix if and only if the given matrix is a square matrix.
• If the inverse of the given matrix and its transpose matrix are similar to each other, then the given square matrix will be known as orthogonal.
• If there is an orthogonal matrix A, then the given matrix A and its transpose matrix A^T will be inverses of each other.
• If we calculate the determinant of an orthogonal matrix, then we will either get 1 or -1 as a result.
• All the identity matrices must be orthogonal matrices.
• In the orthogonal matrix, if we perform the dot product of any two rows or columns, then we will always get 0 as a result.
• There will always be a unit vector in any row or column of an orthogonal matrix.

Examples of Orthogonal matrix

There are a lot of examples of orthogonal matrices, and some of them are described as follows:

Example 1: In this example, we have a matrix A, and we have to determine whether this matrix is an orthogonal matrix. The elements of matrix A are described as follows: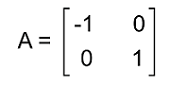

Solution: We can determine whether the given matrix is an orthogonal matrix or not with the help of two ways. In the first way, we will check whether the transpose of matrix A and the inverse of matrix A are similar to each other. In the second way, we will check whether we will get the identity matrix as the multiplication of the given matrix and its transpose matrix. So here we will use the second way.

From the question, we have a matrix A where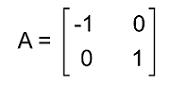

The transpose of the above matrix is described as follows: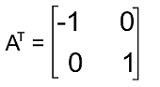

Now we will multiply the matrix A and its transpose matrix A and get the following: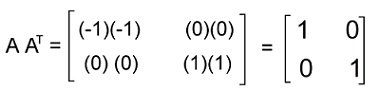

We can see that we get an identity matrix as a result.

Hence matrix A is an orthogonal matrix.

Example 2: In this example, we have a 2∗2 matrix A, and we have to determine whether it is an orthogonal matrix or not.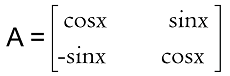

Solution: In the section on properties of the orthogonal matrix, we have already learned that the determinant of orthogonal matrix must be ±1. Now we will calculate the determinant of matrix A in the following way:

|A| = cos x∗cos x - sinx∗(-sin x)

|A| = cos² x + sin² x (From trigonometry we know that cos² x + sin² x = 1)

|A| = 1

The determinant of matrix A is 1.

Hence matrix A is an orthogonal matrix.

Example 3: In this example, we have a 3∗3 matrix P. Here we have to calculate whether the given matrix is an orthogonal matrix without performing any calculations. The elements of matrix P are described as follows: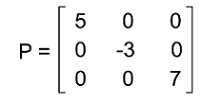

Solution: The given matrix P is a diagonal matrix because the upper triangular elements and the lower triangular elements of this matrix are equal to 0 except for the principal diagonal elements.

When we do the transpose of matrix P, then the given matrix P and its transpose matrix will be similar to each other.

As we have learned that there is a symmetric matrix if the given matrix and its transpose matrix are similar to each other. We also know that if there is a symmetric matrix, then it will be an orthogonal matrix.

Hence matrix P is an orthogonal matrix.

Example 4: In this example, we have an orthogonal matrix A with an order 3. Here we have to determine the inverse of this orthogonal matrix. The elements of this matrix are described as follows: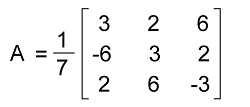

Solution: First, we will determine the transpose of the given matrix in the following way: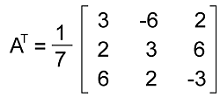

We will get the inverse of this matrix if

A∗A^T = I

Now

Similarly, we can also prove that A^T∗A = I.

Hence it is proved that A is orthogonal.

Then A^-1 = A^T,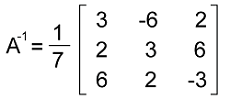

Answer: We have proved the matrix A to be orthogonal with an order 3∗3 and A^-1 =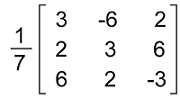

Example 5: In this example, we have to prove whether every orthogonal matrix is symmetric or not. We also have to justify our answer with the help of an example.

Solution: The matrix A will be known as the symmetric matrix if it satisfies the following condition:

A = A^T

For this, we will assume an orthogonal matrix A, which contains the following elements: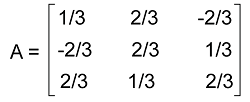

(We can prove that this matrix is orthogonal by proving AA^T = A^TA = I).

Now we will perform the transpose of the assumed matrix A and get the following: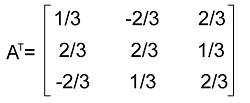

(We can prove it AA^T = A^TA = I).

So we can say that the given matrix and its transpose matrix are not similar to each other, i.e.,

A ≠ A^T

Answer: Every orthogonal matrix will not always be Symmetric.

Example 6: In this example, we have an orthogonal matrix A, and we have to determine (AA^T)^-1. The elements of matrix A are described as follows: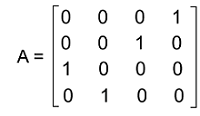

Solution: From the question, we know that the given matrix A is an orthogonal matrix, i.e.,

AA^T = I.

Now we will add inverse on both sides of the above equation like this:

(AA^T)^-1 = I^-1.

As we have learned that the inverse of an identity matrix will be itself. So

I^-1 = I.

Now we will put this in the above equation and get the following:

(AA^T)^-1 = I

Answer: (AA^T)^-1 = I, which is an identity matrix

Example 7: In this example, we have a matrix A, and we have to determine whether it is an orthogonal matrix or not. The elements of matrix A are described as follows: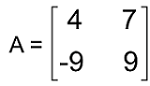

Solution: Here, we will check whether the given matrix is an orthogonal matrix or not with the help of checking the determinant of matrix A. So we will see whether the determinant of given matrix is equal to 1 or not. If it is equal to 1, then it will be an orthogonal matrix.

|A| = 4∗9 - (-9)∗7

|A| = 36 + 63

|A| = 99 ≠ 1.

Thus matrix A is not an orthogonal matrix.