Traversing Binary TreesTraversing means to visit all the nodes of the tree. There are three standard methods to traverse the binary trees. These are as follows:
1. Preorder Traversal: The preorder traversal of a binary tree is a recursive process. The preorder traversal of a tree is
2. Postorder Traversal: The postorder traversal of a binary tree is a recursive process. The postorder traversal of a tree is
3. Inorder Traversal: The inorder traversal of a binary tree is a recursive process. The inorder traversal of a tree is
Example: Determine the preorder, postorder and inorder traversal of the binary tree as shown in fig: 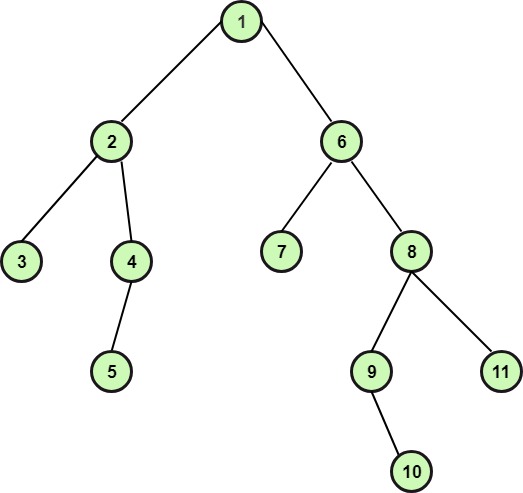
Solution: The preorder, postorder and inorder traversal of the tree is as follows:
Algorithms:(a)Algorithm to draw a Unique Binary Tree when Inorder and Preorder Traversal of the tree is Given:
Example: Draw the unique binary tree when the inorder and preorder traversal is given as follows:
Solution: We know that the root of the binary tree is the first node in preorder traversal. Now, check A, in the inorder traversal, all the nodes that are of left A, are nodes of left subtree and all the nodes that are right of A, are nodes of right subtree. Read the next node in the preorder and check its position against the root node, if its left of the root node, then draw it as a left child, otherwise draw it a right child. Repeat the above process for each new node until all the nodes of the preorder traversal are read and finally we obtain the binary tree as shown in fig: 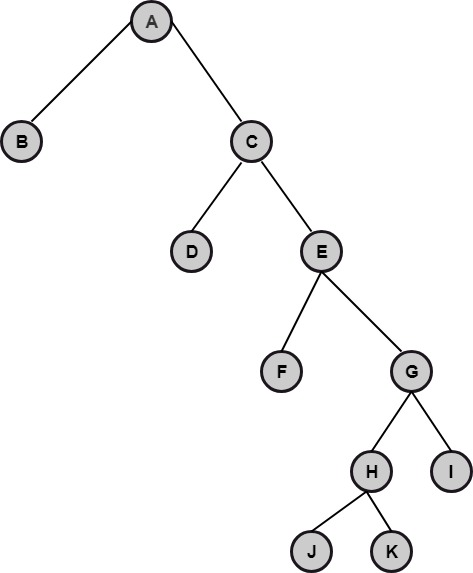 (b) Algorithm to draw a Unique Binary Tree when Inorder and Postorder Traversal of the tree is Given:
Example: Draw the unique binary tree for the given Inorder and Postorder traversal is given as follows:
Solution: We know that the root of the binary tree is the last node in the postorder traversal. Hence, one in the root node. Now, check the inorder traversal, we know that root is at the center, hence all the nodes that are left to the root node in inorder traversal are the nodes of left subtree and, all that are right to the root node are the nodes of the right subtree. Now, visit the next node from back in postorder traversal and check its position in inorder traversal, if it is on the left of root then draw it as left child and if it is on the right, then draw it as the right child. Repeat the above process for each new node, and we obtain the binary tree as shown in fig: 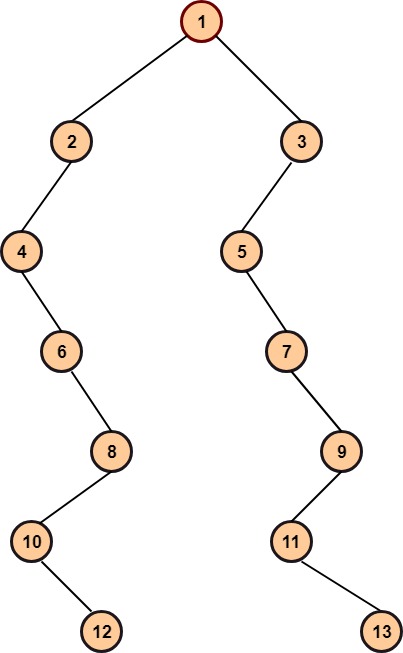 (c)Algorithm to convert General Tree into the binary tree
Example: Convert the following tree as shown in fig into a binary tree. 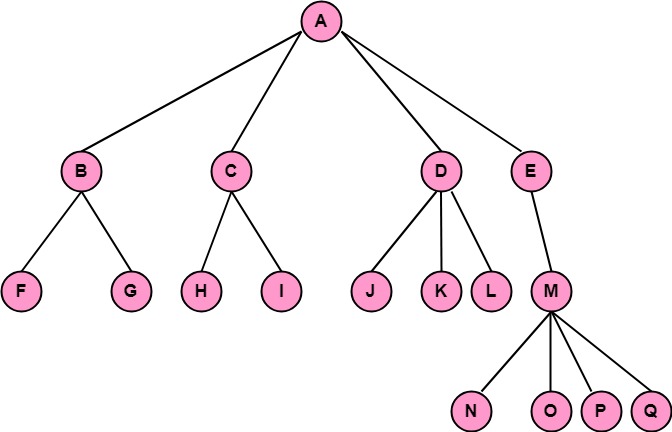
Solution: The root of the tree is the root of the binary tree. Hence A is the root of the binary tree. Now B becomes the left child of A in a binary tree, C becomes the right child of B, D becomes right child of C, and E becomes the right child of D in the binary tree and similarly applying the algorithm we obtain the binary tree as shown in fig: 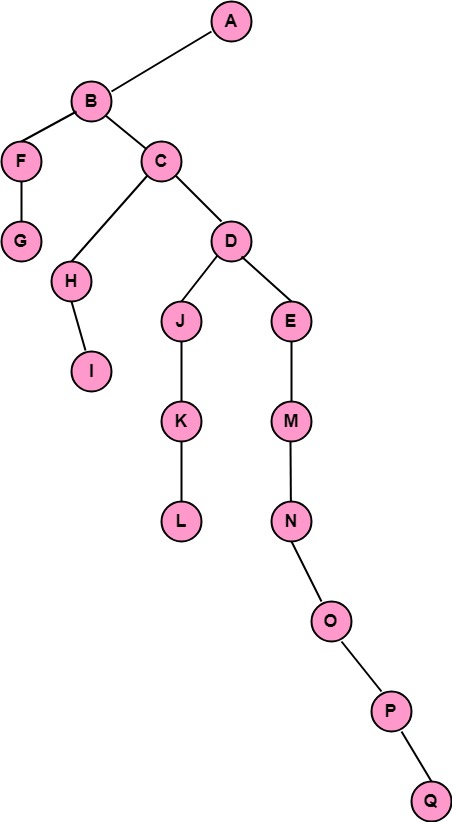
Next TopicBinary Search Trees
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










