Graph:Graph G consists of two things: 1. A set V=V(G) whose elements are called vertices, points or nodes of G. 2. A set E = E(G) of an unordered pair of distinct vertices called edges of G. 3. We denote such a graph by G(V, E) vertices u and v are said to be adjacent if there is an edge e ={u, v}. 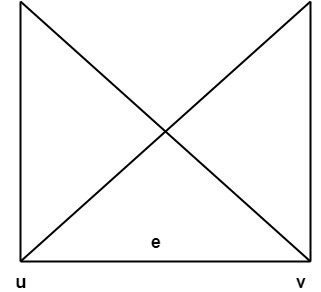
4. In such a case u and v are called the endpoint of e={u, v} and e are said to connect u and v. Degree of a Vertex:The degree of a vertex is the number of edges incident on a vertex v. The self-loop is counted twice. The degree of a vertex is denoted by d(v). Example1: Consider the graph G shown in fig. Determine the degree of each vertex. 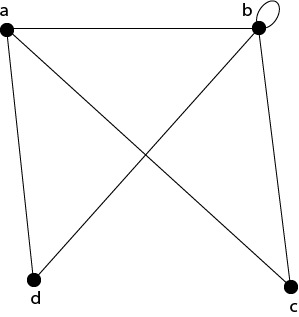
Solution: The degree of each vertex is as follows: d(a)=3; d(b)=5; d(c) = 2; d(d)=2. Example2: Verify that the sum of the degrees of all the vertices is even for the graph shown in fig: 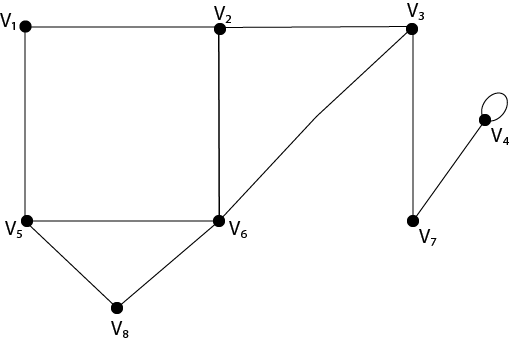
Solution: The sum of the degrees of all the vertices is: =d (v1)+d(v2 )+d(v3 )+d(v4 )+d(v5 )+d(v6 )+d(v7 )+d(v8) Example3: Verify that there are even numbers of vertices of odd degrees in the graph shown in fig: 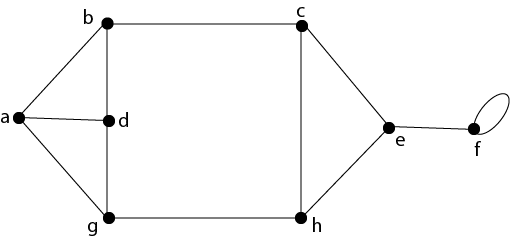
Solution: The number of vertices of degree odd is 8, and each has a degree three in the above graph. Hence, we have even number of vertices of odd degrees. Path:A path of length n is a sequence of n+1 vertices of a graph in which each pair of vertices is an edge of the graph.
Example: Consider the graph shown in fig: Give an example of the following:
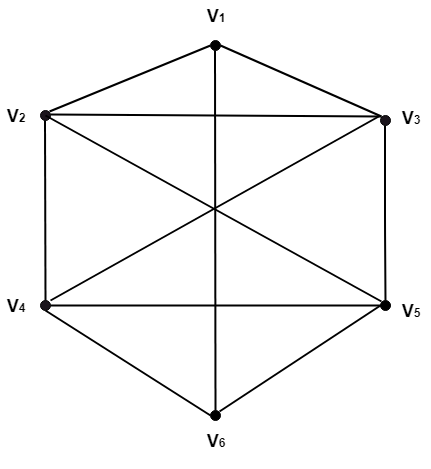
Solution:
Pendant Vertex: A vertex with degree one is called a Pendant Vertex. Pendant Edge: The only edge which is an incident with a pendant vertex is called the Pendant Edge. Odd Vertex: A vertex having degree odd is called an odd vertex. Even Vertex: A vertex having a degree even is called an even vertex. Incident Edge: An edge is called incident with the vertices is connects. Adjacent Vertices: Two vertices are called adjacent if an edge links them. If there is an edge (u, v), then we can say vertex u is adjacent to vertex v, and vertex v is adjacent to vertex u. Example: Consider the graph as shown in fig: 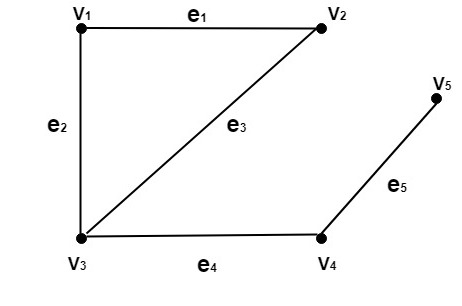
Determine the following:
Solution:
Self-Loop: A self-loop is an edge e if it has the same endpoint. The graph shown in fig contains the self-loop at vertex b,i.e., e=(b, b). Isolated Vertex: A vertex with degree 0 is called Isolated Vertex. 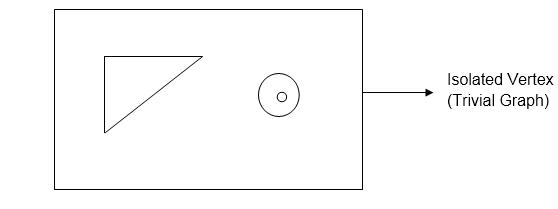
Cut Set: Consider a graph G=(V, E).A cut set for G is the smallest set of edges such that the removal of the set, disconnected the graph whereas the removal of any proper subset of this set left a connected subgraph. Example: Consider the graph shown in fig. Determine the cut set for this group. 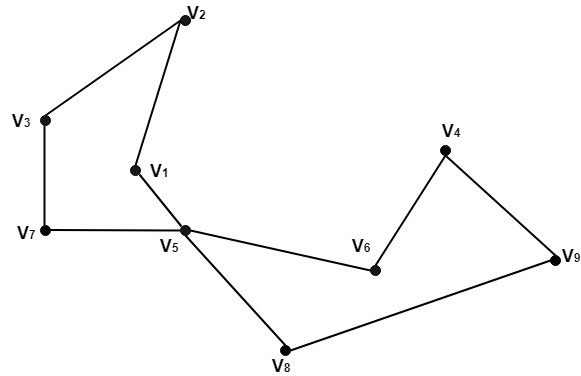
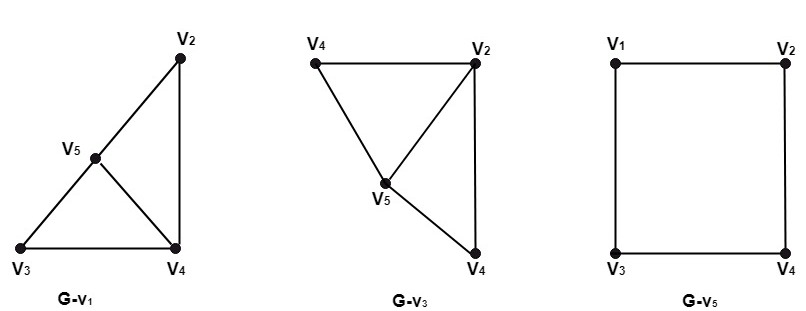
Solution: For this graph, the edge set {(V1,V5),(V7,V5)} is a cut set. After the removal of the set, we have left with a disconnected subgraph. While after the removal of any of its proper subset, we have left with a connected subgraph. Cut Points or Cut Vertices: Consider a graph G=(V, E). A cut point for a graph G is a vertex v such that G-v has more connected components than G or disconnected. The subgraph G-v is obtained by deleting the vertex v from graph G and also deleting the entire edges incident on v. Example: Consider the graph shown in fig. Determine the subgraphs (i)G-v1 (ii) G-v3 (iii) G-v5 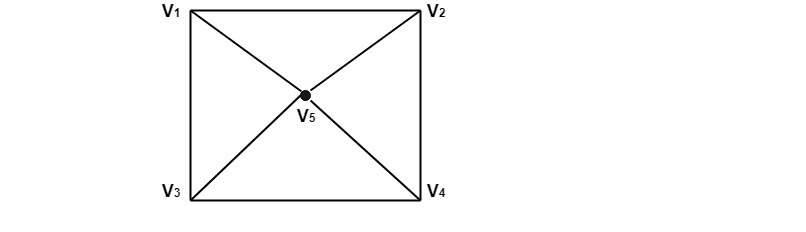
Solution:
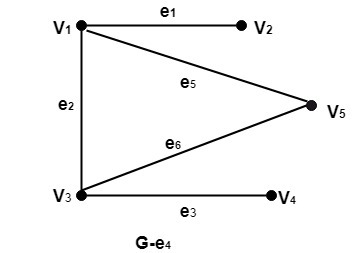
Bridge (Cut Edges): Consider a graph G=(V, E).A bridge for a graph G, is an edge e such that G-e has more connected components than G or disconnected. Example: Consider the graph shown in fig. Determine the subgraphs (i)G-e1 (ii) G-e3 (iii) G-e4 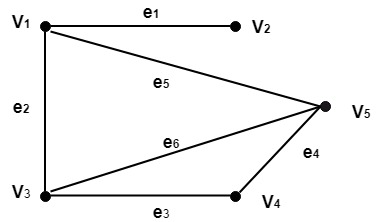
Solution:
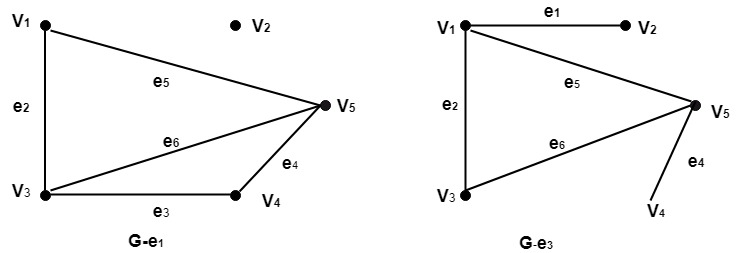 
Next TopicTypes of Graphs
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










