Discrete mathematics for Computer Science

Discrete mathematics is used to provide good knowledge across every area of computer science. In computer science, the applications of discrete mathematics are very vast and described as follows:

Boolean algebra

The bits like one or zero is used to represent all data of the computer at a most fundamental level. Computers perform the calculations when they do some modification in these bits in accordance with Boolean algebra law, which is used to form all digital circuits. The graph is used to represent that digital circuit.

The logical operators like 'and', 'or', and 'not' are used to develop low-level programming languages. When software developers develop any project, they mostly prefer high-level languages. Sometimes they want to optimize their code by reducing the low-level operations, and sometimes, they also directly operate on bits. Programmers can also control the program flow by using Boolean logic. That means they can define certain conditions and then control which instructions will be executed.

Boolean algebra has various laws, which is described as follows:

Commutative law:

According to commutative law, if we change the sequence of variables, it will not affect the result. An operation will be known as commutative operation if it contains the following expression:

1. A.B = B.A
2. A + B = B + A

Associative law:

According to associative law, if we rearrange the parenthesis of any binary expression, it will not change the result of the logical circuit. A binary operation will be known as an associative operation if it contains the following expression:

1. (A.B).C = A.(B.C)
2. (A + B) + C = A + (B + C)  

Distributive law:

According to distributive law, if we multiply a number by the group of numbers added together will have the same result if we perform each multiplication separately. An operation will be known as distributive if it contains the following expression:

A.(B + C) = A.B + A.C

AND law:

If the binary operation uses AND, it will be known as AND law, which is described as follows:

1.	A.0 = 0
2.	A.1 = A
3.	A.A = A
4.	A.Ā = 0 

OR law:

If the binary operation uses OR, it will be known as OR law, which is described as follows:

1.	A + 0 = A
2.	A + 1 = 1
3.	A + A = A
4.	A + Ā = 1  

Inverse Law:

According to inverse law, if we perform double inversion of any variable, it will be output the original variable itself. This law uses the Not operation. An operation will be known as inverse if it contains the following expression:

A + Ā+= 1

Boolean algebra also has De morgan's theorem, which has two laws:

De morgan's First law

According to the first law, the complement of product of variables and the sum of their individual complements of variable is equal to each other, which is described as follows:

 (A.B) = A + B  

De morgan's Second law

According to the second law, the complement of sum of variables and the product of their individual complements of variable is equal to each other, which is described as follows:

(A+B) = A.B

Example of Boolean Algebra

In this example, we will solve the expression C + BC.

We can write the above expression as below on the basis of Demorgan's law:

C + (B + C)

Now we will use the commutative law like this:

(C + C) + B

After that, we will use complement law like this:

1 + B = 1

Therefore,

C + BC = 1

Probability

Probability is used in the field of quantitative as well as in computer science. Probability is used in software engineering to assess the amount of risk. For example, suppose we are designing a system, and we are using probability. In this case, the probability will tell about the capacity of the system that means how much load our system can handle, and after that peak load, the system will crash. We can also measure the network's reliability using probability. In machine learning, we can do tasks ranging from developing good medical treatment to calibration of spam filters using various conditional probability applications.

A randomized algorithm is known as the more efficient and best algorithm when it comes to practice because they provide the exact computing of those tasks that are difficult to compute. Probability can be described as one of the foundations of data science as well as statistics. It is also known as one of the hottest fields in the industry. If students are studying probability on the basis of computer science, it will provide them a quantitative intuition, and it is useful in their everyday life and throughout their careers. We have the formula to specify the probability,

Probability of event to happen P(E) = Number of favorable outcomes/Total Number of outcomes

Example of Probability

Suppose there are 6 suits in a shop, in which 3 are green, 2 are purple, and 1 is orange. We will find the probability to pick an orange suit.

Solution:

The probability will be calculated by dividing the number of orange suits in a shop by the total number of suits. So

2/6 = 1/3 

Propositional Logic

When a developer develops any project, it is important that he should be confident of getting desired results by running their code. We can use mathematics to describe the programs. The reason for their correctness is propositional logic tools. The core area of computer science is known as algorithms, and it is difficult to analyze and design an algorithm by using these critical skills. The principle of mathematical induction is used by the two major paradigms: functional programming and iterative programming. This principle is used to verify their loops and recursive function calls separately.

The most formal specification language can be called Logic used in the foundation and design of programming language. For instance, languages in the SQL family are just the implementation of relational logic, which has some added features. Some particular logic calculus and many domain specific languages have the same implementation. In industry, there is an increment of adoption of formal methods and program verification. It is also used in tandem with techniques of traditional testing to increase confidence about the performance and effectiveness of the software.

Examples of propositional logic:

3+3=5
Narendra Modi is the Prime Minister.
'a' is a vowel. 

This example has three sentences that are propositions. Where the first sentence is False or invalid, and the last two sentences are True or Valid.

Some examples are not propositional, which is described as follows:

1 + a = 5
Go on vacation and enjoy

This example has two sentences that are not propositions because the first sentence may be false or true because the value of 'a' is not specified, so we can't say that it is true or false unless we specify the value and the last sentence don't have a truth value.

Induction and Recursion

If we want to know the functional paradigm of programming, the key concepts which will be used are induction and recursion. Recursion is a type of programming strategy, which is used to solve large problems. We will split the large problem into smaller problems of the same kind. While induction is a type of mathematical strategy, which is used to prove statements related to large sets of things.

Many industries and companies like Facebook (Haskell), Amazon, Microsoft research(F*, Haskell), Apple(Swift), Oracle(JavaScript, Java 8), and Microsoft(F#) increases the adoption of functional paradigm for the general use and niche tasks. Data structure and algorithm can also be easily described using the Recurrences. In the theoretical area of computer science and many computation models, they are treated as a backbone. The more critical part, especially in the sensitive application, is the security properties of software and correctness.

Example of induction:

Using the mathematical induction, show n < 2ⁿ for all positive integer n.

Solution:

We will assume that proposition of n is P(n): n < 2ⁿ

Basic step: P(1) is true since 1 < 2¹

Inductive step: If P(n) is true then for each n P(n+1) is true.

We will assume that P(n): n < 2ⁿ is true

Then we will show P(n+1): n+1 < 2ⁿ⁺¹ is true.

n + 1 < 2n+ 1
< 2n + 2n
= 2n(1 + 1)
 = 2n(2)
= 2n+1

Example of recursion:

Example 1:

We will describe the example of recursive defined function:

f(0) = 5
f(n) = f(n-1) + 2

Solution:

We will calculate the function's value like this:

f(0) = 5
f(1) = f(0) + 2 = 5 + 2 = 7
f(2) = f(1) + 2 = 7 + 2 = 9
f(3) = f(2) + 2 = 9 + 2 = 11 

This recursively defined function is equivalent to an explicitly defined function, which is described as follows:

f (n) = 2n + 5

Example 2:

We will describe the example of recursive defined function:

f(0) = 0
f(n) = f(n-1) + 2n-1 

Solution:

We will calculate the function's value like this:

f(0) = 0
f(1) = f(0) + (2)(1) -1 = 0 + 2 - 1 = 1
f(2) = f(1) + (2)(2) -1 = 1 + 4 - 1 = 4
f(3) = f(2) + (2)(3) -1 = 4 + 6 -1 = 9 
f(4) = f(3) + (2)(4) -1 = 9 + 8 -1 = 16 

This recursively defined function is equivalent to an explicitly defined function, which is described as follows:

f (n) = n2

Number Theory

In the number theory, we will learn about the sets of positive whole numbers that can be 1, 2, 3, 4, 5, 6, etc. They are also known as the set of natural numbers. In number theory, our main focus is to learn the relationship between various sorts of numbers. In the field of computer security, cryptography, and blockchain, the critical applications are contained by the Number theory. According to mathematics, the user's data is perfectly secured from the various types of attacks and malicious adversaries with the help of a modern cryptographic system.

The mathematical basis for hashing is described by modular arithmetic, and it is the most useful tool for several applications. The files which are transferred by the internet are verified by the Checksum, and it is based on hashing. Data structures like hash map perform efficient operations by using modular arithmetic. In the operating system and computer architecture, number theory also provides the facility to use memory-related things. There are many familiar and non-familiar examples of number theory, which is described as follows:

Even: 2, 4, 6, 8, 10, 12?..
Odd: 1, 3, 5, 7, 9??
Triangular: 1, 3, 6, 10, 15, 21?..
Prime: 2, 3, 5, 7, 11, 13, 17??
Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21?..
Square: 1, 4, 9, 16, 25?.
Cube: 1, 8, 27, 64??.
Perfect: 6, 28, 496?.

Counting

We can also develop quantitative intuitions by using Counting techniques. For example, suppose the users create passwords by using some defined set of rules. Now we can get the number of valid passwords by using the counting technique. This technique is also used to determine the time duration taken by an attacker to brute force all the passwords. Now we will learn the pigeonhole principle, which describes why we don't have an algorithm that can describe universal lossless compression. When we use a compression algorithm, it decreases certain files every time and increases the number of other files. Different types of files, such as video, audio, text, images, etc, can be compressed by using each compression algorithm. The complexity of algorithm can be easily determined with the help of counting.

The real-world application has a lot of different available resources that have a complicated tradeoff. Some tasks don't have a lot of space that's why they have to sacrifice their time for more space, while others require a fast algorithm because they can afford a huge space to achieve the speed. In a complex situation, we require to achieve a sweet spot in resource usages so that the system does not face the problem related to resource starvation and keeps running perfectly. Using counting, we are able to create these considerations in a structural manner. It can also provide a formal guarantee related to resource usage.

Examples of Counting

Example 1:

In this example, we will calculate that how many 3-digit numbers can be formed from 2, 3, 4, 5 7, and 9 digits.

Solution: As we can see that there are 6 available digits. So

(6)(6)(6) = 216

Example 2:

Suppose Jack goes to a pizza shop and chooses to create his own pizza. The shop has 4 different kinds of sauces, 4 different kinds of breads, and 3 different kinds of cheese, but he can only choose one of each category. Now we have to find that how many different ways a pizza can be created.

Solution:

(4)(4)(3) = 48

Graphs

A Graph can be described as a pictorial representation of the set of objects in which links are used to connect some pair of objects. It is a group of vertices and edges. Where vertices are used to represent interconnected objects, which is denoted by V. The edges are a type of link, which is used to connect the vertices, and it is denoted by E. Graph is known as a powerful data structure.

The graph has the ability to answer questions and model the relationship. For example, when we use our navigation app to search for the fastest route from our office to our home, this app uses the graph search algorithm to search it. It will also show us the time during according to our vehicle. The graph is extensively used in computer science to represent a file system. It is also used in database, deep learning, functional programming, and other applications.

Examples of Graphs:

Example 1: Suppose there is a pair of sets (V, E), where V is used to contain the set of vertices and E is the set of edges, which is used to connect the pairs of vertices. Now we will consider the following graph and find the number of vertices and edges.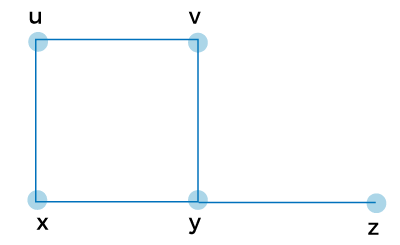

In this graph,

V = {u, v, w, x, y}
E = {uv, uw, vx, wx, xy}

Example 2: We have to find the vertices and edges of the following graphs.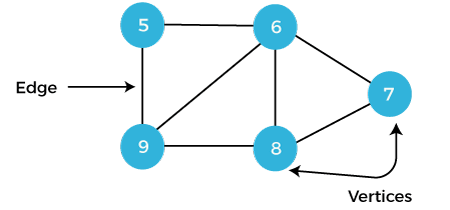

In this graph,

V = {5, 6, 7, 8, 9}
E = {56, 67, 78, 89, 59, 69, 68}