Irrational Number in Discrete mathematics

Irrational numbers can be described as real numbers. We cannot represent those types of real numbers as the ratio of integers. In other words, the irrational number can also be described as those real numbers that are not rational. For example: √ 5 is an irrational number.

Definition of Irrational numbers

The set of real numbers is contained by the irrational number, and these types of numbers will never be expressed as fraction such as p/q. Here p is used to show the numerator, q is used to indicate the denominator, and both are integers. Here q must not be equal to 0, i.e., q ≠ 0. The examples of irrational numbers are √ 7 and √5, etc. If there is a decimal expansion of irrational numbers, then it will neither be repeating nor terminating. Whereas, if any number is expressed in the form of x/y, and y ≠ 0 and x and y both are integers, then these numbers will be called the rational numbers.

Representation of Irrational number

It can be described as real numbers that cannot be expressed in the form of a simple fraction. With the help of symbol "\", we can indicate the irrational numbers, i.e., R\Q. Here, \ is called the backward slash symbol, which is used to show "set minus". We can also indicate it as R- Q, which basically describes the difference between a set of real numbers and a set of rational numbers.

If we try the calculations on the basis of irrational numbers, then it will be a little bit complicated. For example: √11, √7, √13 etc, all are irrational numbers. If there is an arithmetic operation in which these numbers are used, then we will first solve the values under root. Even after that, the values of irrational can also be sometimes recurring.

Meaning of irrational

The irrational means no ratio. It means that the irrational number cannot have a ratio. We can only use the roots to indicate the irrational number, and we cannot express it in any other way. We can also not express these types of numbers as the ratio of two integers.

Symbol of Irrational number

The word "P" is used to indicate the symbol of an irrational number. The irrational number and rational number are contained by the real numbers. Since, we have defined the irrational number negatively. So the irrational number can be defined as a set of real numbers (R), which cannot be a rational number (Q). Due to the association of rational number and the real number, because the association contains the alphabetic sequence P, Q, R, so we have used the symbol P to indicate the irrational number. But we mostly represent the irrational number with the help of difference between a set of real numbers (R) and a set of rational numbers (Q). So we can use the following way to write the irrational numbers like this:

R - Q or R \Q.

Hence, the symbol P shows the irrational number.

Common examples of Irrational numbers

There are some specific types of irrational numbers, which we have mostly used while finding the irrational numbers, which are described as follows:

Pi(π):πis known as the irrational number. The value of pi is 3.14159265. The value of decimal cannot be stopped at any time. Since, the π's value and the fraction 22/7 are similar to each other. So we can also take the π's value as 3.14 or 22/7.

Note: The number 22/7 is known as the rational number.

√2: The square root of 2 or √2 is known as an irrational number. Suppose there is a right-angled isosceles triangle, which has two sides, AB and BC, which are equal to each other, and the length of these sides is 1 unit. With the help of Pythagoras theorem, we know that the hypotenuse AC will be √2 = 1⋅414213….

Euler number:Euler number is indicated by e, which is equal to the number 2.718281…

Golden ratio:Golden ratio is indicated by φ, which is equal to the number 1.61803398874989….

Properties of Irrational numbers

There are a lot of properties related to irrational numbers, which will be useful to find out the irrational numbers from the given real number's set. Some properties of irrational numbers are described as follows:

• There will be non-recursive decimals and the non-terminating in the irrational numbers.
• The irrational numbers can only be the real numbers.
• If we try to add a rational number and an irrational number, then it will generate the result in the form of an irrational number only. Suppose there is a rational number y and an irrational number x, then their sum will be x + y = an irrational number.
• If we try to multiply the irrational number and any non-zero rational number, then it will generate the result in the form of an irrational number. Suppose there is a rational number y and an irrational number x, then their multiplication will be x*y = irrational number
• There may or may not be the LCM in any two given irrational numbers. Here, LCM can be specified as the least common multiplication.
• If we perform the addition, division, multiplication, or subtraction operations on the two irrational numbers, then the generated result may or may not be rational numbers. For example: √2 * √2 = 2. Here √2 is used to indicate the irrational number.
• In the process of multiplication, the irrational number's set cannot be closed. But in the case of rational numbers, they are closed.

Set of Irrational numbers

We can obtain the set of irrational numbers with the help of writing some irrational numbers with brackets. There are some properties that will help to determine the set of irrational numbers, which are described as follows:

• If the square roots of the real numbers are not perfect square, then that number will be an irrational number. For example: √2, √3, √5, √8.
• There are some famous irrational numbers, i.e., Pi, Golden ratio, and Euler's number {e, ?, ?}.
• If we do the square root of any prime number, then their result will be the irrational number.

The list of irrational numbers is described in the following table:

Rational VS Irrational numbers

The rational number can be defined by those types of numbers, which can be indicated as the fraction p/q or ratio. The rational number can contain integers or whole numbers. In the rational number, p is the numerator, and q is the denominator, where p must not be equal to zero.

• 2/3 = 0.6666 = 0.67. As we can see that the decimal value is recursive (repeating). That's why we approximated it to 0.67.
• √4 = 2 and -2, where 2 and -2 are used to indicate the integers.

The difference between irrational numbers and rational numbers is described as follows:

Interesting facts about Irrational Numbers

The irrational number is used to contain a lot of cool and interesting facts, which are described as follows:

1. Accidental Invention of √2:

√2, or the square root of 2, is known as the irrational number.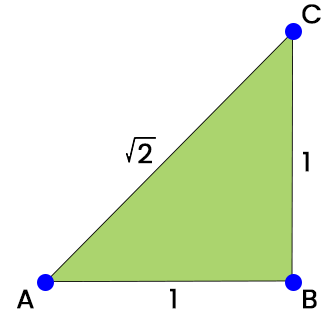

The first invented irrational number at the time of processing of calculating the isosceles triangle's length is the square root of 2 or √2. To calculate it, a famous Pythagoras formula is used, which is described as follows:

a² = b² + c²

AC² = AB² + BC² ? AC² = 1² + 1² ? AC = √2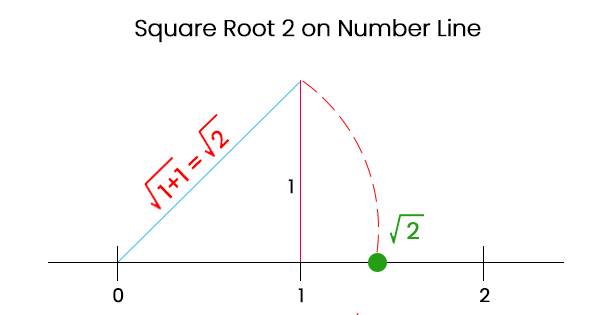

As we know that the value of √2 is 1.41421…. This is because √2 lies between 1 and 2 numbers. So he revealed that we could not express the length of AC as integers or fractions.

2. The value of π

When we calculate the π's value, we have found approx 22 trillion digits which do not have an end. In order to calculate the value of π, a computer usually takes approx 15 days with 24 hard drives.

3. Inventions of Euler's number e:

A Swiss mathematician Leonhard Euler was introduced the concept of Euler's number in 1731. We can also call 'e' as Napier's number. We can use this number 'e' in the field of logarithm and trigonometry.

Addition and Multiplication of two Irrational Numbers

Here we will learn about the addition and multiplication of two irrational numbers. First we will discuss the multiplication of two irrational numbers and after that, we will learn the sum of two irrational numbers.

Product of two irrational numbers

Statement: If we perform the multiplication operation upon two irrational numbers, then it will either generate the rational or irrational numbers as a result.

For example:

Suppose there is an irrational number √2, and if we multiply √2 by √2, then we will get 2 as a result. Where, 2 is a rational number. So,

√2 * √2 = 2

Suppose there is an irrational number Π, and if we multiply Π by Π, then we will get Π² as a result, which is an irrational number. So,

Π * Π = Π²

So we have concluded that when we multiply two irrational numbers, then we can either get the irrational number or rational number as a result.

Addition of two irrational numbers

Statement: If we perform the addition operation upon two irrational numbers, then it will generate a rational or irrational number as a result.

Just like the multiplication of above two irrational numbers, the addition of two irrational numbers also generates the same output in the form of rational numbers or irrational numbers.

For example: Suppose there are two irrational numbers, 3√2+ 4√3, and if we add these numbers, then their addition will be an irrational number.

But suppose there are two irrational numbers, +4√2 and -4√2 and if we add those numbers, then we will get 3 as a result which is a rational number.

So if we multiply or add two irrational numbers, then we need to take care because the result of these operations can be a rational number or an irrational number.

Theorem and Proof of Irrational number

We can prove the above statements relating to the addition and multiplication with the help of below theorem:

Theorem: Suppose there is a prime number p and a² is divided by p, then it will be concluded that p also divides a.

Proof:With the help of Fundamental Theorem of arithmetic, we can express the positive integers with the help of products of its primes, which are described as follows:

a = p1 * p2 * p3 * p4 …. * pn ……(1)

Here p1, p2, p3, p4 …., pn is used to indicate all the prime factors of a.

Now we will do squaring of both sides of the above equation (1) in the following way:

a² = (p1 * p2 * p3 * p4 …. * pn) (p1 * p2 * p3 * p4 …. * pn)

? a² = (p1)² * (p2)² * (p3)² * (p4)² …. * (pn)²

On the basis of the Fundamental Theorem of Arithmetic, we know that there is a unique prime factorization of the natural numbers except for the order of its factors.

p1, p2, p3, p4 …., pn are used to contain only the prime factor of a². If there is a prime number p and a factor of a², in this case, p will be one of p1, p2, p3, p4 …., pn. So, p is also a factor of a.

Hence, it concludes that if p divides a², then p will also divide a.

With the help of this theorem, we can also prove that √2 is irrational.

Finding of Irrational number:

Here we have to determine the irrational number between 2 and 3.

As we know that, 2 is the square root of 4, i.e., √4 = 2, and 3 is the square root of 9, i.e., √9 = 3.

Therefore, √5, √6, √7, and √8 are called as the number of irrational numbers. These numbers are irrational numbers because these numbers cannot be further simplified and also do not contain perfect squares. In the same way, if we want to determine the irrational number between any other two perfect square numbers, then we can also do that.

Another Case:

Suppose there is a case of √2. Now we have to determine whether the given number √2 is an irrational number or not.

Now we will consider that √2 is a rational number. Then we can write this number in the following way with the help of definition of rational numbers like this:

√2 = p/q ….. (1)

Here p and q are used to indicate the co-prime integers, and q must not be equal to 0, i.e., q ≠ 0. (The given number will be co-prime number if the common factor of the given numbers is 1).

Now we will do square on both sides of the equation (1) in the following way:

2 = p² /q²

? p² = 2q² ….. (2)

With the help of above theorem, we know that if 2 is a prime factor of p², in this case, 2 will also be a prime factor of p.

On the basis of the starting assumption, we know that p and q both are co-prime, but we get the output from above contradicts on the basis of this assumption as p and q do not contain 1 as the common prime factor, but it contains 2. Only because of the incorrect assumption that √2 is rational, this contradiction of the common prime factor as 2 has occurred.

So, root 2 (√2) is irrational.

In the same way, we can also prove the statement, which we have discussed in the starting that if there is a prime number p, then √p will also be an irrational number. Similarly, we can also prove that √p is irrational for any prime number p.

Examples of Irrational numbers

Example 1: In this example, we have 5 numbers, and we have to determine which numbers are irrational and rational numbers.

1. 2
2. -.45678…
3. 6.5
4. √2
5. √3

Solution:

-2, 6.5, both the numbers contain the terminating decimals. That's why these numbers are rational numbers.

-.45678…, √2, √3 all contain the non-repeating or non-terminating decimal expansion. That's why these numbers are irrational numbers.

Example 2: In this example, we have 4 numbers, and we have to determine which numbers are irrational and rational numbers.

1. 2
2. 5/11
3. -5.12
4. 0.31

Solution: 2, 5/11, -5.12, 0.31, all numbers contain the terminating decimal expansion. That's why these numbers are rational numbers.

Important Points

• If we do the multiplication of any two irrational numbers, then it will either be a rational number or an irrational number. For example: We will get an irrational number if we multiply √2 and Π. The result of this multiplication will be 4.4428829. There is one more example: if we multiply √2 and √2, then we will get an rational number, i.e., 2.
• At the time of multiplication operation, the set of irrational numbers must not be closed. But in the case of rational number, it will be closed.
• If we perform the addition and multiplication of two given irrational numbers, then it may be generated a rational number as a result. For example: If we multiply the square root of 2 (√2) with again the square root of 2, then it will generate a rational number 2, i.e., √2 * √2 = 2. Here, √2 is used to indicate the irrational number. So, in conclusion, we know that if we multiply it twice, then the result of this multiplication will be a rational number, i.e., 2.