Properties of Binary OperationsThere are many properties of the binary operations which are as follows: 1. Closure Property: Consider a non-empty set A and a binary operation * on A. Then is closed under the operation *, if a * b ∈ A, where a and b are elements of A. Example1: The operation of addition on the set of integers is a closed operation. Example2: Consider the set A = {-1, 0, 1}. Determine whether A is closed under
Solution: (i)The sum of elements is (-1) + (-1) = -2 and 1+1=2 does not belong to A. Hence A is not closed under addition. (ii) The multiplication of every two elements of the set are -1 * 0 = 0; -1 * 1 =-1; -1 * -1 = 10 * -1 = 0; 0 * 1 = 0; 0 * 0 = 0 1 * -1 = -1; 1 * 0 = 0; 1 * 1 = 1 Since, each multiplication belongs to A hence A is closed under multiplication. 2. Associative Property: Consider a non-empty set A and a binary operation * on A. Then the operation * on A is associative, if for every a, b, c, ∈ A, we have (a * b) * c = a* (b*c). Example: Consider the binary operation * on Q, the set of rational numbers, defined by a * b = a + b - ab ∀ a, b ∈ Q. Determine whether * is associative. Solution: Let us assume some elements a, b, c ∈ Q, then the definition (a*b) * c = (a + b- ab) * c = (a + b- ab) + c - (a + b- ab)c= a + b- ab + c - ca -bc + abc = a + b + c - ab - ac -bc + abc. Similarly, we have Therefore, (a * b) * c = a * (b * c) Hence, * is associative. 3. Commutative Property: Consider a non-empty set A,and a binary operation * on A. Then the operation * on A is associative, if for every a, b, ∈ A, we have a * b = b * a. Example: Consider the binary operation * on Q, the set of rational numbers, defined by a * b = a2+b2 ∀ a,b∈Q. Determine whether * is commutative. Solution: Let us assume some elements a, b, ∈ Q, then definition a * b = a2+b2=b * aHence, * is commutative. 4. Identity: Consider a non-empty set A, and a binary operation * on A. Then the operation * has an identity property if there exists an element e in A such that a * e (right identity) = e * a (left identity) = a ∀ a ∈ A. Example: Consider the binary operation * on I+, the set of positive integers defined by a * b = Determine the identity for the binary operation *, if exists. Solution: Let us assume that e be a +ve integer number, then e * a, a ∈ I+ Similarly, a * e = a, a ∈ I+ From equation (i) and (ii) for e = 2, we have e * a = a * e = a Therefore, 2 is the identity elements for *. 5. Inverse: Consider a non-empty set A, and a binary operation * on A. Then the operation is the inverse property, if for each a ∈A,,there exists an element b in A such that a * b (right inverse) = b * a (left inverse) = e, where b is called an inverse of a. 6. Idempotent: Consider a non-empty set A, and a binary operation * on A. Then the operation * has the idempotent property, if for each a ∈A, we have a * a = a ∀ a ∈A 7. Distributivity: Consider a non-empty set A, and a binary operation * on A. Then the operation * distributes over +, if for every a, b, c ∈A, we have 8. Cancellation: Consider a non-empty set A, and a binary operation * on A. Then the operation * has the cancellation property, if for every a, b, c ∈A,we have
Next TopicSemiGroup
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





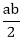
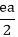 = a, e = 2...............equation (i)
= a, e = 2...............equation (i)




