Bayes Formula for Conditional probabilityThe Bayes theorem states that the probability of an event is based on prior knowledge of the conditions that might be related to the event. It is also used to examine the case of conditional probability. If we are aware of conditional probability, we can use the Bayes formula to calculate reverse probabilities. Let's understand this concept with the help of an example. Suppose we have to determine the probability of taking a black ball from the second bag out of three different bags of balls, where each bag contains three different balls such as red, blue, black. In such a case, the probability of occurrence of an event is calculated depending on other conditions is called conditional probability. In this article, we will discuss the statement and proof of Bayes theorem, formula, derivation with examples. 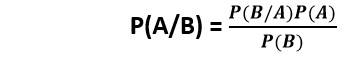
The probability of A occurring given that event B has taken place is equal to the product of the probability of event A occurring at all and the probability of event B taking place given that event A has taken place, divided by the probability of event B taking place at all. If you toss two coins, what's the probability they both come up tails? There are four possible outcomes; Coin 1: Heads, Coin 2: Heads Coin 1: Heads, Coin 2: Tails Coin 1: Tails, Coin 2: Heads Coin 1: Tails, Coin 2: Tails Only one of these outcomes is the same thing as "both coming up tails." Therefore, there's a one in four chance that we'll get two tails, and this is the basic example of simple probability. Where the "conditional" part comes in is where we start throwing additional information into the mix. So now, let's ask the question: "what's the probability that we'll get two heads given that coin 1 came up heads?" Going through this: Coin 1: Heads, Coin 2: Heads Coin 1: Heads, Coin 2: Tails So, there's a one in two chance of two heads given the condition that coin 1 comes up heads. Statement of Bayes TheoremLet E1, E2, E3,…….En is a set of events related with a sample space S, where all the events E1, E2, E3,…….En have a non-zero probability of occurrence, and they form a partition of S. Suppose A be the event-related with sample space S, then according to Baye theorem. 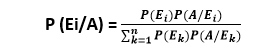
For variable k = 1,2, 3,…..n Proof of Bayes theoremAccording to the conditional probability formula 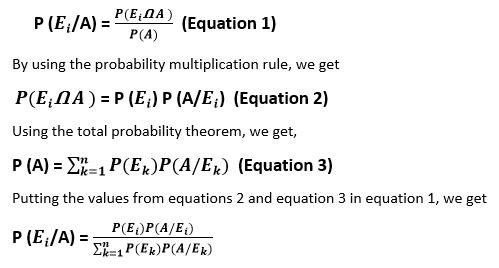
Examples based on Bayes theorem Example 1 A bag P contains 6 white and 6 blue balls, while another bag Q contains 3 white and 3 blue balls. One ball is randomly drawn from one of the bags, and it is found to be blue. Calculate the probability that it was drawn from bag P. Solution: Let E1 be the event of selecting bag P, E2 be the event of selecting bag Q, and A be the event of drawing a blue ball. Then, P (E1) = P (E2) = ½ Also, P(A/E1) = P (Drawing a blue ball from bag P) = 6/12 = ½ P(A/E2) = P (Drawing a blue ball from bag Q) = 3/6 = ½ Using the Bayes theorem, the probability of drawing a blue ball from bag P out of two bags P and Q is given below. 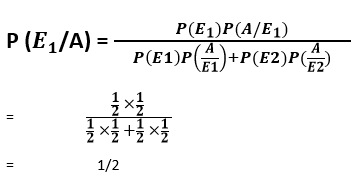
Example 2 A man is known to speak the truth 3 times out of 5. He throws a dice and reports that the number he has got is a five. Calculate the probability that the number obtained is actually a five. Solution: Let A be the event that the man reports that number five is obtained. Let E1 be the event that four is obtained and E2 be its complimentary event. Then, P (E1) = Probability that five occurs = 1/6 P (E2) = Probability that five does not occur = 1 - P(E1) = 1 - 1/6 = 5/6 Also, P (A/E1) = Probability that man reports five, and it is a five = 3/5 P (A/E2) = Probability that man reports five, and it is not a five, = 2/5 By using Bayes theorem, the probability that number obtained is actually a five, 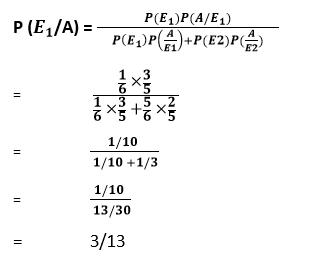
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









