Diagonal matrix in Discrete mathematicsIf we want to learn about the diagonal matrix in discrete mathematics, then for this, we have to first discuss a little bit about few types of matrices. So we will learn about triangular matrices. We have two types of triangular matrices i.e., upper triangular matrices and lower triangular matrices. Both types of matrices are described as follows: A matrix will be known as the lower triangular matrix if there is a square matrix in which all the elements which are contained above the principal diagonal are zeros. The example of a lower triangular matrix is described as follows: 
A matrix will be known as the upper triangular matrix if there is a square matrix in which all the elements which are contained below the principal diagonal are zeros. The example of a upper triangular matrix is described as follows: 
In this section, we are going to learn about diagonal matrix, their properties, anti-diagonal matrix, the determinant of a diagonal matrix, the inverse of a diagonal matrix, diagonalization of a matrix, block diagonal matrix, examples of a diagonal matrix, and many more things. What is diagonal matrixMatrix will be known as the diagonal matrix if it contains both upper triangular and lower triangular. That means if all the elements which are exit above and below the principal diagonal are zero, then this type of matrix will be a diagonal matrix. That means a matrix will be known as the diagonal matrix if all the elements of the matrix are zero except the principal diagonal. The principal diagonal can contain any value. According to the mathematical definition, a matrix A = [aij] will be known as the diagonal matrix if it contains the two conditions, which are described as follows:
For example: 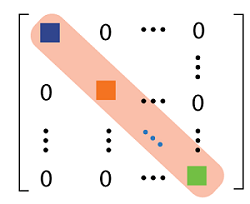
If the principal diagonal contains 0, then this type of matrix will also be a diagonal matrix because according to the condition of a diagonal matrix, all the elements other than the diagonal must be 0. That means it will not matter whether the diagonal contains 0 as an element or not. The matrix will be a diagonal matrix as long as the elements beside diagonal are zero. For example: 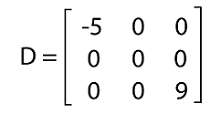
In this matrix, all the elements except the principal diagonal are 0, and it is a square matrix. The elements of principal diagonals are -5, 0, and 9. Hence the matrix D is a diagonal matrix. Examples of Diagonal matrix on the basis of orderHere we will show the square matrices with different orders, which are described as follows: Diagonal matrix of order 2The general form of a diagonal matrix with order 2∗2 is described as follows: 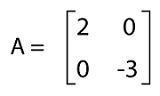
This matrix contains the same number of rows and columns (2∗2). That's why this matrix is a square matrix. The principal diagonal of this matrix contains entries 2 and -3, respectively. All the other entries of this matrix are 0. Hence matrix A is a diagonal matrix. Diagonal matrix of order 3The general form of a diagonal matrix with order 3∗3 is described as follows: 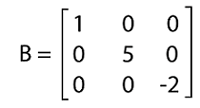
This matrix contains the same number of rows and columns (3∗3). That's why this matrix is a square matrix. The principal diagonal of this matrix contains entries 1, 5, and -2, respectively. All the other entries of this matrix are 0. Hence matrix A is a diagonal matrix. Diagonal matrix of order 4The general form of a diagonal matrix with order 4∗4 is described as follows: 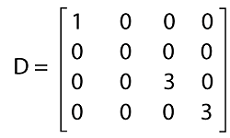
This matrix contains the same number of rows and columns (4∗4). That's why this matrix is a square matrix. Now we can see that one of the diagonal entries (D22) of this matrix is 0. This value is allowed to satisfy the definition of diagonal matrix because, according to the definition, we are only concerned with the off-diagonal entries (that must be 0), and the diagonal matrix is allowed to any value (that can be 0). The principal diagonal of this matrix contains entries 1, 0, 3, and 3, respectively. All the other entries of this matrix are 0. Hence matrix D is a diagonal matrix. Properties of Diagonal matrixThere are a lot of properties of the diagonal matrix, and some of them are described as follows: Property 1:If there are two diagonal matrices that contain the same order, then only after the addition or multiplication operation we will get the resultant diagonal matrix. For example: Suppose there are two diagonal matrices, P and Q, where the elements of P and Q are described as follows: 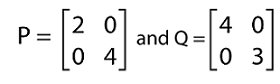
The addition of P and Q is described as follows: 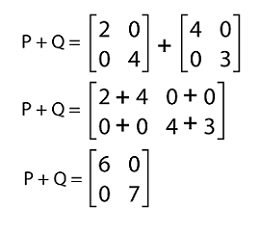
Property 2:If we do the transpose of a diagonal matrix, then the original matrix will be the resulting diagonal matrix. That means D = DT. For example: 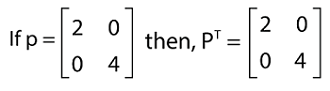
Property 3:The diagonal matrices are commutative at the time of multiplication operation. For example: Suppose there are two diagonal matrices, P and Q where 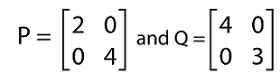
The multiplication of PQ is described as follows: 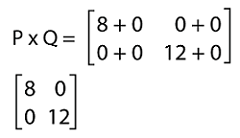
The multiplication of QP is described as follows: 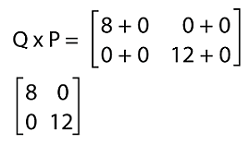
In the above result, we can see that PQ = QP. Hence the diagonal matrices are commutative under multiplication. Property 4:The diagonal matrices are commutative at the time of addition operation also. For example: Suppose there are two diagonal matrices, P and Q where 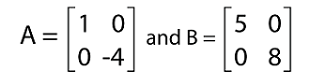
The addition of A and B is described as follows: 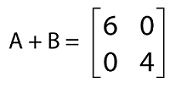
The addition of B and A is described as follows: 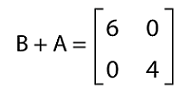
In the above result, we can see that A + B = B + A. Hence the diagonal matrices are commutative under addition. Some more PropertiesThere are some more properties related to the diagonal matrix, which are described as follows:
For example: Suppose there are two diagonal matrices, A and B where 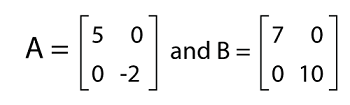
The multiplication of these matrices is described as follows: 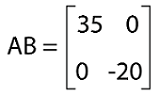
Determinant of Diagonal matrixBy doing the multiplication of diagonal elements of the diagonal matrix, we can calculate the determinant of that diagonal matrix. Suppose there is a matrix A, and we have to determine the determinant of that matrix. The elements of matrix A are described as follows: 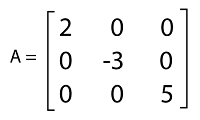
det A = 2(-15 - 0) - 0(0 - 0) + 0(0 - 0) = -30. This is known as the multiplication of principal diagonal elements 2, -3, and 5. Thus, 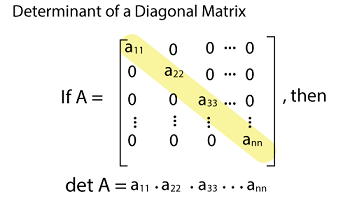
If all the principal diagonal elements of the diagonal matrix are non-zero, in this case, the diagonal matrix will be a non-singular matrix. Inverse of a diagonal matrixWe will get a diagonal matrix as a result of the inverse of a diagonal matrix. In this matrix, principal diagonal elements will be reciprocal of the corresponding elements of the original matrix. The formula to calculate the inverse of a diagonal matrix is described as follows: D-1 = 1/|D|∗(adj D) Now we will understand this with the help of some examples. Example 1: Suppose there is a matrix D, where 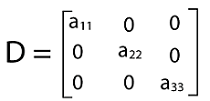
Now we will determine the determinants of this matrix D like this: 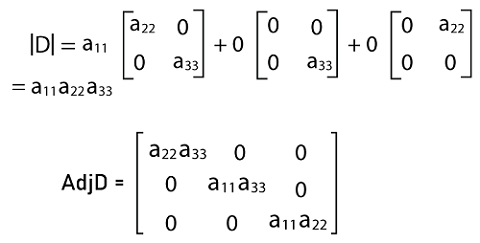
Now we will put these values into the formula of inverse matrix, which is described as follows: D-1 = 1/|D|∗(adj D) = 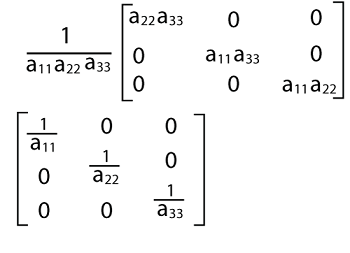
Example 2: Suppose there is a 3∗3 diagonal matrix. Here we have to find the adjoint of this matrix. The elements of diagonal matrix are described as follows: 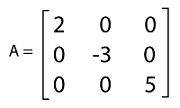
Solution: To determine the adjoint matrix, we will first determine the determinant of the given matrix like this: det A = 2(-15 - 0) - 0(0 - 0) + 0(0 - 0) = -30 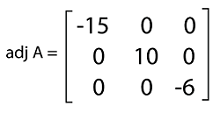
The inverse of given matrix A is A-1 = (adj A)/ (det A). Now we will put the value of adj A and det A in this equation and get the following: 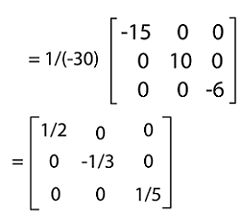
The above matrix A-1 is also a diagonal matrix. Here we can also see that the principal diagonal elements are the reciprocals of the corresponding elements of A. Thus, 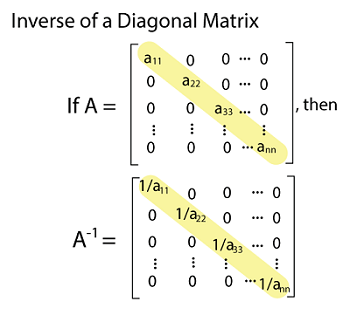
Block diagonal matrixA matrix will be known as the block matrix if it is split into the block matrix. This type of square matrix is used to contain zero matrices in the off-diagonal blocks and the main diagonal blocks square matrices. That means the non-diagonal blocks are 0. The matrix D will be known as the block diagonal matrix if there is a case where Dij = 0 and i ? j. The block diagonal matrix with an order n∗n is described as follows: 
Anti diagonal matrixThe anti-diagonal matrix and the diagonal matrix both have a mirror image in case of the placement of elements. A matrix will be known as the anti-diagonal matrix if the entries of this matrix are 0 in the lower left corner to the other upper side corner of the diagonal, except those entries which occur on the diagonal. In other words, we can say that this type of matrix contains zero in the upper and lower part of the diagonal elements. If there is any anti-diagonal matrix, then it must be a non-diagonal matrix. The anti-diagonal matrix must be in the following form: 
The example of an anti-diagonal matrix is described as follows: 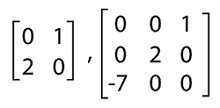
Diagonalization of matrixIf there is a square matrix A and we want to do diagonalization of this matrix, then it will be written in the following way: A = XDX-1 Where D is used to indicate the diagonal matrix, which is formed with the help of eigenvalues of A, and X is formed with the help of corresponding eigenvectors of A. Suppose there are eigenvalues of matrix A, λ1, λ2, λ3, ....., λn. In this case, the diagonal matrix D and X will be described as follows: 
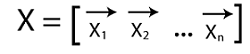
Here 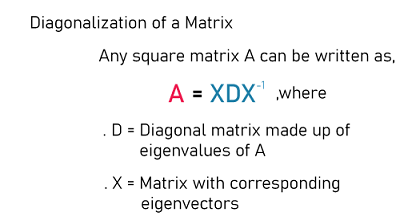
Important notes on diagonal matrixThere are some notes which we should know while learning the concept of a diagonal matrix, which are described as follows:
Examples of Diagonal matrixThere are a lot of examples of diagonal matrices, and some of them are described as follows: Example 1: In this example, we have to check whether the multiplication of a diagonal matrix and a non-diagonal matrix will be a diagonal matrix. Solution: For this, we will assume a diagonal matrix A and a non-diagonal matrix B, which contains the following elements: 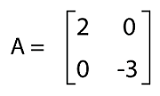
And 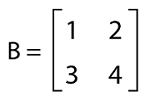
Now we will perform the multiplication of both the matrices, A and B, like this: 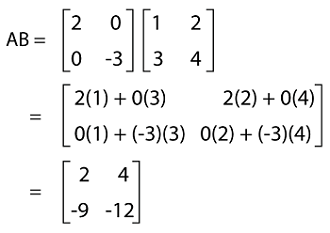
In this resultant matrix, we can see that the multiplication of AB is not a diagonal matrix. Hence the multiplication of a diagonal matrix and a non-diagonal matrix will NOT be a diagonal matrix. Example 2: In this example, we have a matrix C, and we have to determine whether this matrix is a diagonal matrix or not. The elements of matrix C are described as follows: 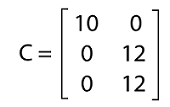
Solution: This matrix contains the 3 number of rows and 2 number of columns. That means the number of rows and columns are not similar to each other. That's why this matrix is not a square matrix. Hence this matrix cannot be a diagonal matrix. Example 3: In this example, we have a matrix A, and we have to determine the determinant of this matrix. The elements of matrix A are described as follows: 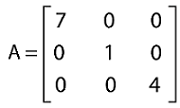
Solution: We can see that matrix A is a diagonal matrix. This is because the determinant of this matrix can be calculated by the multiplication of elements of its diagonal. So det A = 7(1)(4) = 28 Hence the determinant of A is 28. Example 4: In this example, we have two matrices, A and B, and we have to add these matrices. We have to also determine whether the resultant matrix is a diagonal matrix or not. The elements of A and B are described as follows: 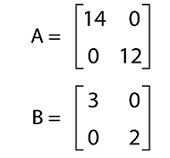
Solution: From the question, we have the following matrices: 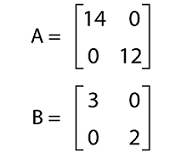
The addition of A and B is described as follows: 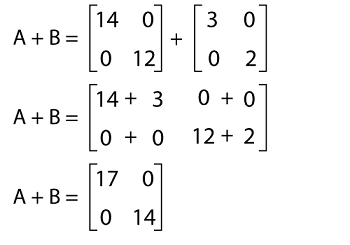
From this resultant matrix, we can see that all the elements except diagonal elements are zero. Hence when we perform the addition of above matrices, A and B, then we get a diagonal matrix as a resultant matrix. Example 5: In this example, we have two matrices, A and B, and we have to multiply these matrices. We have to also determine whether the resultant matrix is a diagonal matrix or not. The elements of A and B are described as follows: 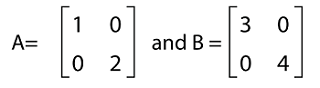
Solution: From the question, we have the following matrices: 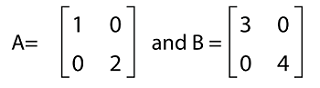
The multiplication of AB is described as follows: 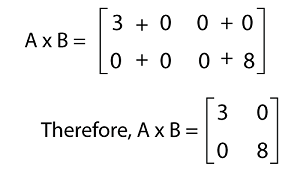
From this resultant matrix, we can see that all the elements except diagonal elements are zero. Hence when we perform the multiplication of above matrices, A and B, then we get a diagonal matrix as a resultant matrix. Example 6: In this example, we have a matrix A, and we have to determine the inverse of this matrix. The elements of this matrix are described as follows: 
Solution: We can see that this matrix is a diagonal matrix. We can get the inverse of a diagonal matrix with the help of replacing all its principal diagonal elements with their reciprocals, and in this process, all the elements except the principal diagonal elements will remain the same. Therefore, the inverse of a given matrix is described as follows: 
Hence the inverse of given diagonal matrix will be: 
Example 7: In this example, we have two diagonal matrices, A and B. We have to show that the multiplication of these matrices is commutative. The elements of matrices A and B are described as follows: 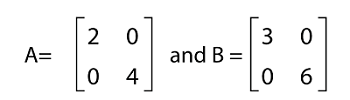
Solution: From the question, we have the following matrices: 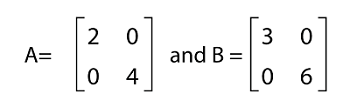
The multiplication of AB is described as follows: 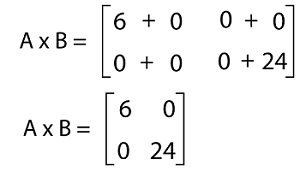
The multiplication of BA is described as follows: 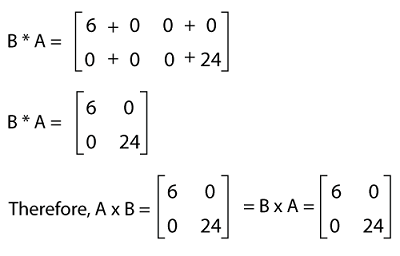
Hence proved the multiplication of diagonal matrices, A and B is commutative. Example 8: In this example, we have a matrix A, and we have to determine the diagonalize of this matrix. The elements of matrix A are described as follows: 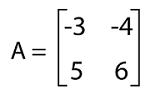
Solution: We can write the diagonalization of a given matrix in the form of multiplication of matrices, XDX-1, where D is used to indicate the diagonal matrix with eigenvalues X is used to show the matrix of corresponding eigenvectors Now we will determine the eigenvalues and eigenvectors one by one, and after that, we will be able to find the inverse of that matrix. Finding Eigenvalues Suppose |A - λ I| = 0, where I used to indicate the identity matrix. 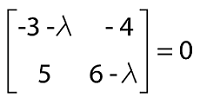
(-3 - λ) (6 - λ) - (-4)(5) = 0 -18 + 3λ - 6λ + λ2 + 20 = 0 λ2 - 3λ + 2 = 0 (λ - 1) (λ - 2) = 0 λ = 1, λ = 2 Thus, 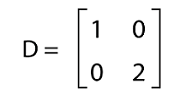
Finding Eigenvectors When λ = 1: A - λ I = A - I 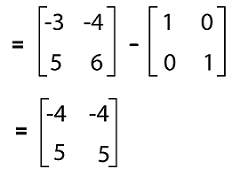
From the above equation, we will get two equations, i.e., -4x1 - 4x2 = 0 and 5x1 + 5x2 = 0 Here we will assume that x2 = 1. Now we will get the value of x1 by putting the value of x2 into the equation 5x1+5x2 = 0 like this: 5x1 + 5 = 0 x1 = -5/5 x1 = -1 So the eigenvector corresponding to λ = 1 is described as follows: 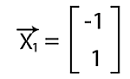
In the same way, we can determine the eigenvector corresponding to λ = 2 in the following way: 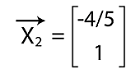
Thus, 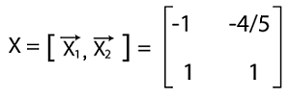
Now we will determine the inverse of this matrix in the following way: 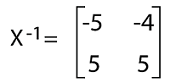
Therefore, A = XDX-1 Now we will put all the calculated values in this equation like this: 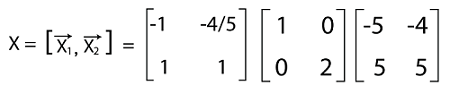
Hence the diagonalization of matrix A is 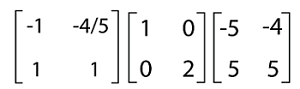
Next TopicSingular matrix in Discrete mathematics
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




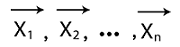 is used to indicate the eigenvectors, which correspond to the eigenvalues λ1, λ2, λ3, ....., λn in order, and it is written in the form of column vectors.
is used to indicate the eigenvectors, which correspond to the eigenvalues λ1, λ2, λ3, ....., λn in order, and it is written in the form of column vectors.




