Representation of RelationsRelations can be represented in many ways. Some of which are as follows: 1. Relation as a Matrix: Let P = [a1,a2,a3,.......am] and Q = [b1,b2,b3......bn] are finite sets, containing m and n number of elements respectively. R is a relation from P to Q. The relation R can be represented by m x n matrix M = [Mij], defined as
Mij = 0 if (ai,bj) ∉ R
1 if (ai,bj )∈ R
Example The matrix of relation R is shown as fig: 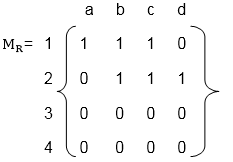 2. Relation as a Directed Graph: There is another way of picturing a relation R when R is a relation from a finite set to itself. Example 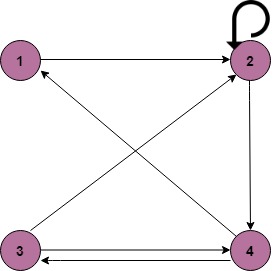 3. Relation as an Arrow Diagram: If P and Q are finite sets and R is a relation from P to Q. Relation R can be represented as an arrow diagram as follows. Draw two ellipses for the sets P and Q. Write down the elements of P and elements of Q column-wise in three ellipses. Then draw an arrow from the first ellipse to the second ellipse if a is related to b and a ∈ P and b ∈ Q. Example The arrow diagram of relation R is shown in fig: 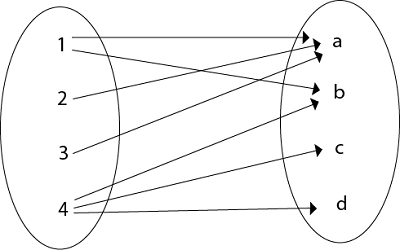 4. Relation as a Table: If P and Q are finite sets and R is a relation from P to Q. Relation R can be represented in tabular form. Make the table which contains rows equivalent to an element of P and columns equivalent to the element of Q. Then place a cross (X) in the boxes which represent relations of elements on set P to set Q. Example The tabular form of relation as shown in fig: 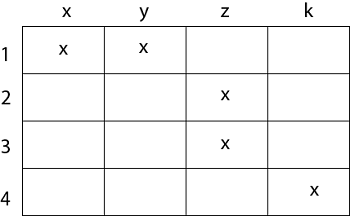
Next TopicComposition of Relations
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










