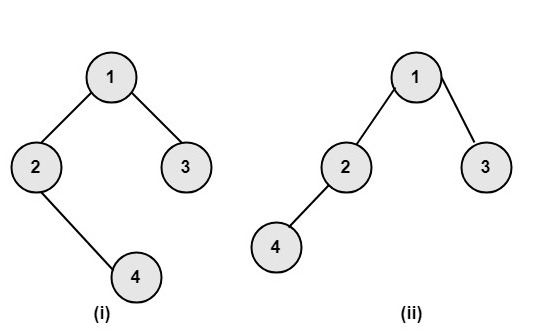
Binary Trees:If the outdegree of every node is less than or equal to 2, in a directed tree than the tree is called a binary tree. A tree consisting of the nodes (empty tree) is also a binary tree. A binary tree is shown in fig: Basic Terminology:Root: A binary tree has a unique node called the root of the tree. Left Child: The node to the left of the root is called its left child. Right Child: The node to the right of the root is called its right child. Parent: A node having a left child or right child or both are called the parent of the nodes. Siblings: Two nodes having the same parent are called siblings. Leaf: A node with no children is called a leaf. The number of leaves in a binary tree can vary from one (minimum) to half the number of vertices (maximum) in a tree. Descendant: A node is called descendant of another node if it is the child of the node or child of some other descendant of that node. All the nodes in the tree are descendants of the root. Left Subtree: The subtree whose root is the left child of some node is called the left subtree of that node. Example: For the tree as shown in fig:
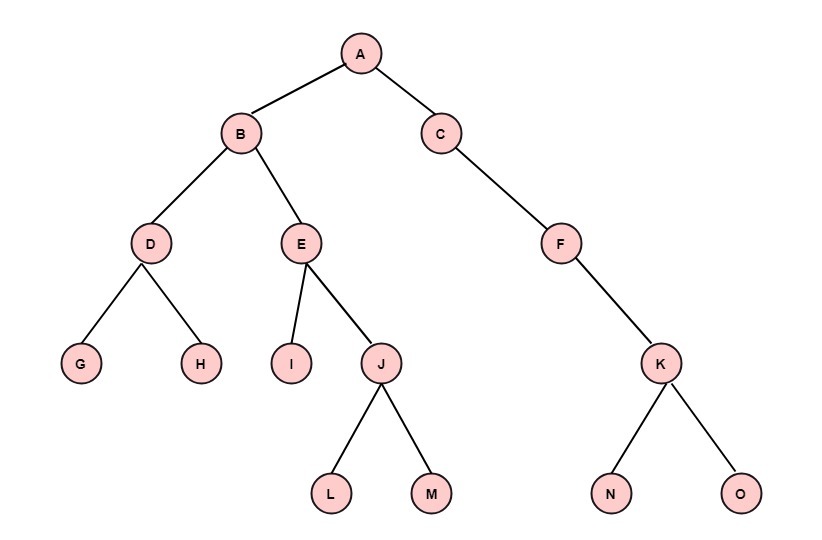
Solution: (i) The node A is the root node. Right Subtree: The subtree whose root is the right child of some node is called the right subtree of that node. Level of a Node: The level of a node is its distance from the root. The level of root is defined as zero. The level of all other nodes is one more than its parent node. The maximum number of nodes at any level N is 2N. Depth or Height of a tree: The depth or height of a tree is defined as the maximum number of nodes in a branch of a tree. This is more than the maximum level of the tree, i.e., the depth of root is one. The maximum number of nodes in a binary tree of depth d is 2d-1, where d ≥1. External Nodes: The nodes which have no children are called external nodes or terminal nodes. Internal Nodes: The nodes which have one or more than one children are called internal nodes or non-terminal nodes. Binary Expression Trees:An algebraic expression can be conveniently expressed by its expression tree. An expression having binary operators can be decomposed into Depending upon precedence of evaluation. The expression tree is a binary tree whose root contains the operator and whose left subtree contains the left expression, and right subtree contains the right expression. Example: Construct the binary expression tree for the expression (a+b)*(d/c) Solution: The binary expression tree for the expression (a+b)*(d/c) is shown in fig: 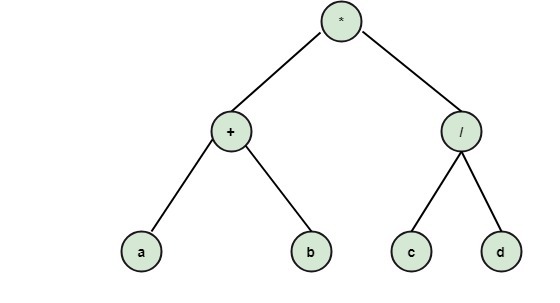
Complete Binary Tree: Complete binary tree is a binary tree if it is all levels, except possibly the last, have the maximum number of possible nodes as for left as possible. The depth of the complete binary tree having n nodes is log2 n+1. Example: The tree shown in fig is a complete binary tree. 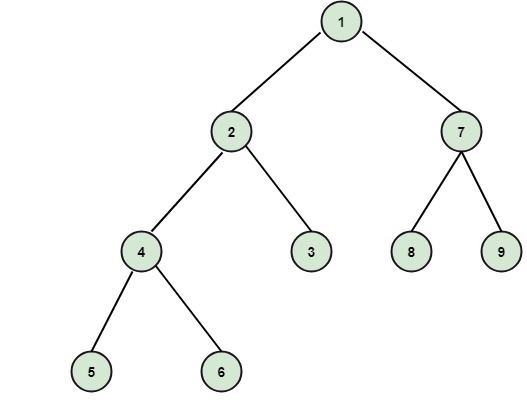
Full Binary Tree: Full binary tree is a binary tree in which all the leaves are on the same level and every non-leaf node has two children. 
Differentiate between General Tree and Binary Tree
Next TopicTraversing Binary Trees
| ||||||||||
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share